On 3/3/17, I was able to work with an outstanding group of 5th graders at a local elementary school on one of my favorite 3-act tasks by Graham Fletcher – The Apple.
The Apple gets students thinking about division as measurement, and if left to solve the problem in a way that makes sense to them, they tend to generate a range of strategies that can be really useful stuff for making connections in a pre-reveal discussion about their strategies. In particular, this task is useful for making connections between:
- repeated addition (adding one block at a time until we ‘arrive’ at the apple’s weight)
- repeated subtraction (taking off a block’s-worth of weight from the apple until we ‘arrive’ at zero)
- multiplication (often in the form of guess and check after students grow weary of repeated addition), and
- fraction division using the common denominator method (get a common denominator and divide the numerators).
We started by playing the video for students and asking them what they noticed and wondered. As they shared, we recorded their noticings and wonderings on chart paper:

As a class, we decided on the starred question as the one to solve for the day. Once we’d come to consensus (using words and gestures) for what it would mean to balance the scale, we asked students to estimate the number of blocks it would take. We recorded their estimates.
We then asked students what information they would need to solve this problem – and why they would need it. Most students suggested fairly quickly that we would need to know the weight of the blocks and the weight of the apple – but I asked several students to argue for why we needed both and not just one. This took some time, but by the end it seemed most students understood why both weights were important, and what significance they had mathematically and contextually.
Then, we gave them the information. (I wrote the info down in the wrong ‘spots’ on the “what do we need to know” chart at first, so I had to rewrite.)

Once we gave them this information, we gave students about 2-3 minutes to begin a strategy on their own piece of paper – enough time to make a plan, but not enough time to follow it all the way through.
After a few minutes passed, we asked them to talk to the other students at their tables and discuss their strategies, and come to a decision about how they would use one or more of the strategies at their tables to solve the problem. They were also tasked with representing one strategy on a group white board. Here’s what those white boards looked like by the end:
Multiplication strategy: what number multiplied by 3/8 gets us 5 and 2/8?
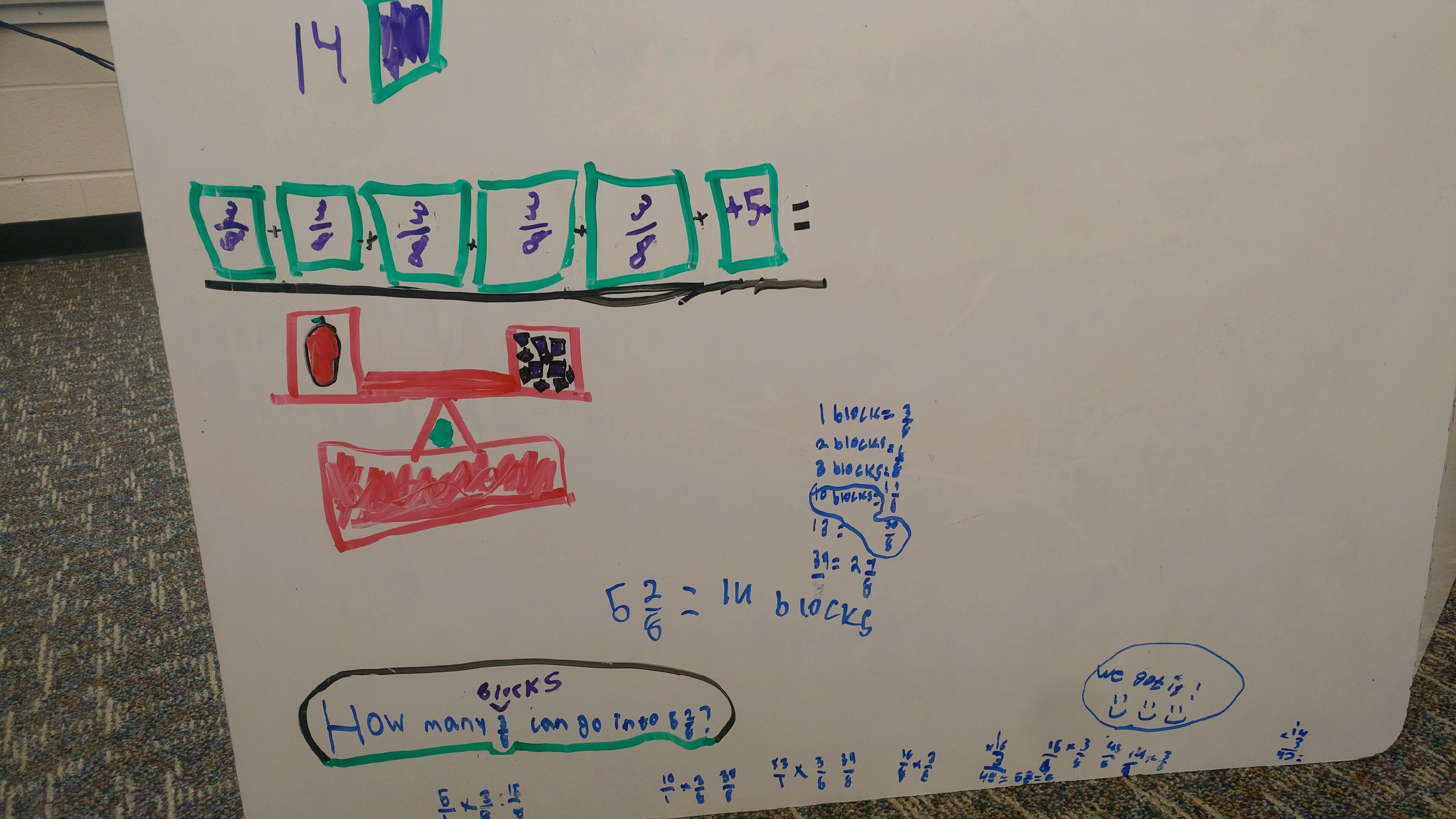
These students started by repeatedly adding 3/8 until they grew weary of it, and decided to start multiplying. They tried 1, 2, 3, 5, 10, 13, and then finally did 13 blocks plus 1 more block.
Repeated addition of 4 blocks at a time.
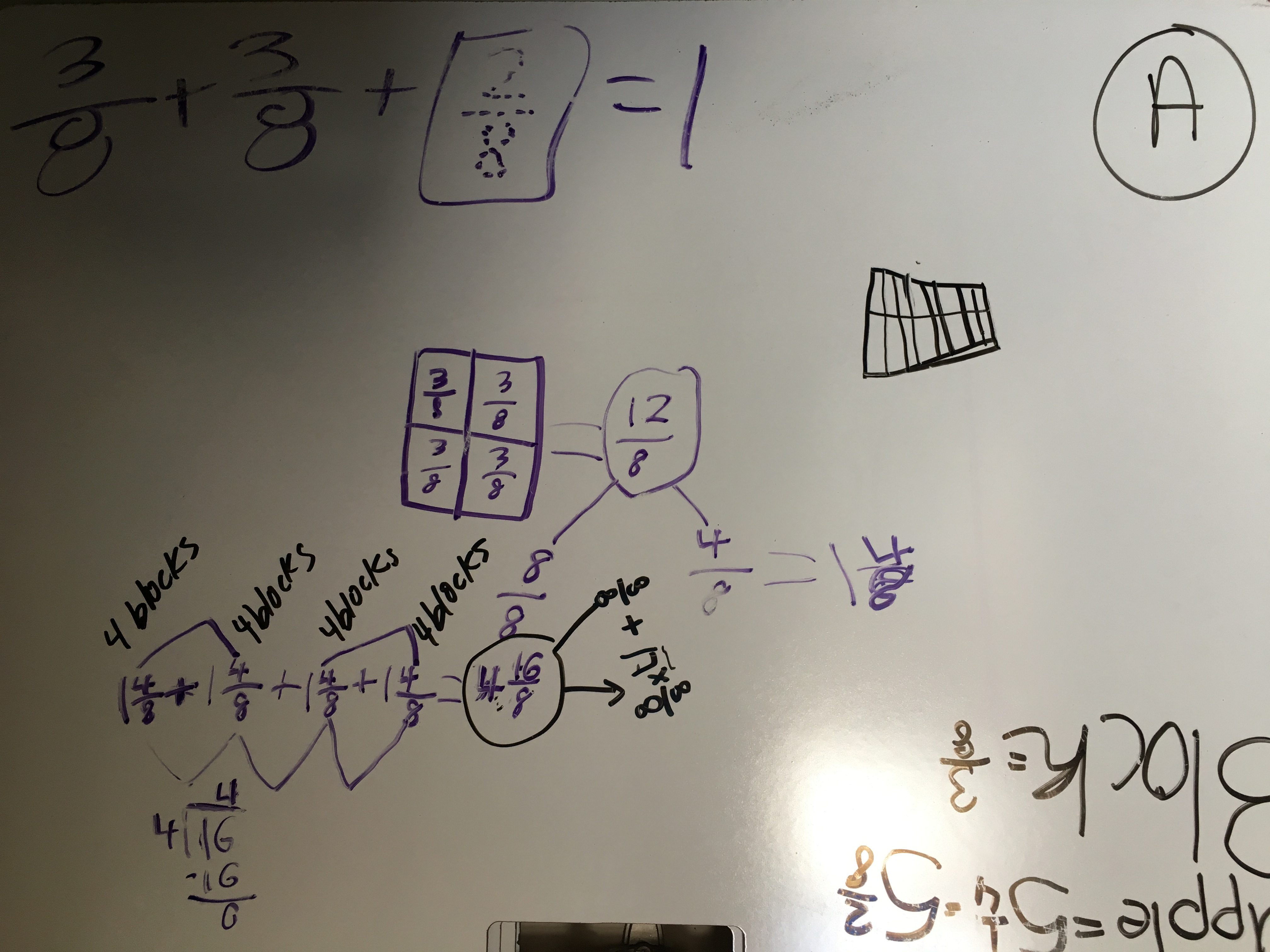 I LOVED this strategy. This group was led by two students in particular whose really wanted to find a combination of blocks that would add up to an easy ‘split.’ So they settled on 4 blocks, since 4 groups of 3/8 makes 12/8, which would only need 1/2 an ounce to get to the next whole. They knew, then, that two groups of 4 blocks would ‘make up’ the next whole.
I LOVED this strategy. This group was led by two students in particular whose really wanted to find a combination of blocks that would add up to an easy ‘split.’ So they settled on 4 blocks, since 4 groups of 3/8 makes 12/8, which would only need 1/2 an ounce to get to the next whole. They knew, then, that two groups of 4 blocks would ‘make up’ the next whole.
Once they started down this path, however, they found themselves in improper fraction land quite quickly, which it turned out was not a land they had adventured in many times before. Out of the 4 students in the group, 3 of them were quite insistent that 4 and 16/8 oz (which they arrived at by repeatedly adding 4 blocks 4 times – so, 16 blocks) was not yet enough weight to equal the apple. They had some difficulty moving past this moment, and ran out of time to come to consensus as a group about what should happen next – though they agreed that it would likely entail adding single blocks to finally get to 5 1/4 oz, since most of them were sure that 4 more would be too many.
Repeated addition, using a choral count representation
This was a strategy we were really hoping would turn up, since the students had just done a choral count by 1/8 in the moments preceding the 3-act task. Interestingly, this strategy did not represent the first strategy all of the students in the group had used; several had used a division strategy, but because they could not figure out how to represent or explain how that strategy worked (which was what we insisted they be able to do with any strategy they put on their board), they resorted to using a repeated addition strategy. The challenging thing in this group’s case was figuring out in all of this representation where the answer was.

In addition to these three group boards, there was one last group who had worked hard to find solution strategies independently, but who had run out of time to get much onto their board before we discussed strategies:
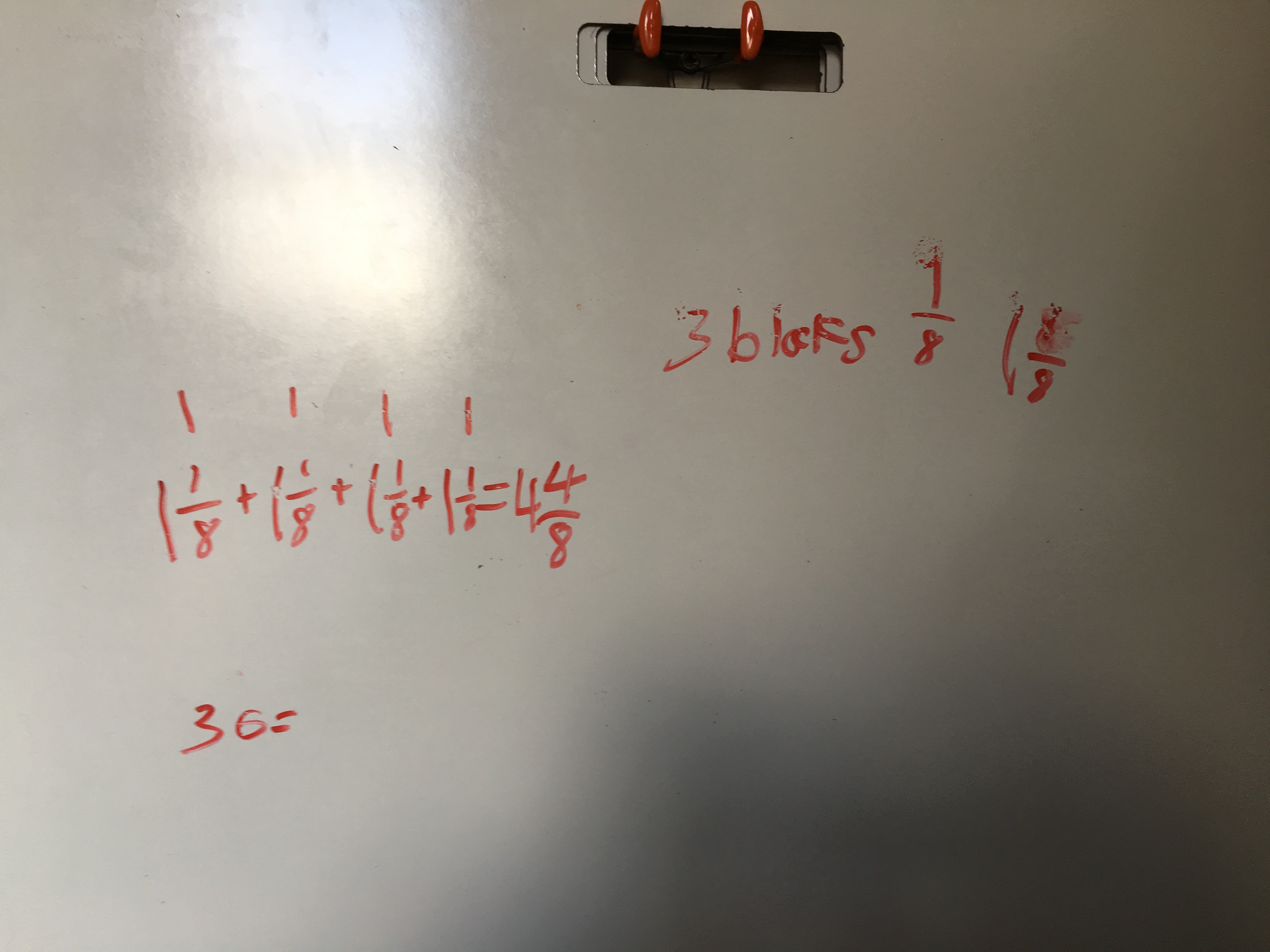
The students had about 20 minutes in their groups to produce the representations above, and then we took about 10 minutes to look across the first three boards above, first looking at the choral count strategy, then the repeated addition of 4 blocks, then finally the multiplication strategy. The questions I asked of each group were –
- where is the apple represented in this group’s strategy?
- How did they know where to stop?
- What were they looking to have happen by [adding 1/8 at a time…adding 4 blocks at a time…multiplying numbers by 3/8]
- How did they know they had done enough?
- Based on all of this work, what is the group’s answer to the question?
Though I’m not confident that all of the students came to consensus about whether or why multiplication was more efficient than repeated addition, they all agreed that in this case, anyway, it produced the same result. The group who was adding ‘batches’ of 4 blocks at a time seemed to understand by the end that their method was functioning pretty well, but that it might require more adjustment because of undershooting or overshooting the perfect amount – a problem the choral count group didn’t have, but that the multiplication group did (they found that 13 was close, so they adjusted from there).
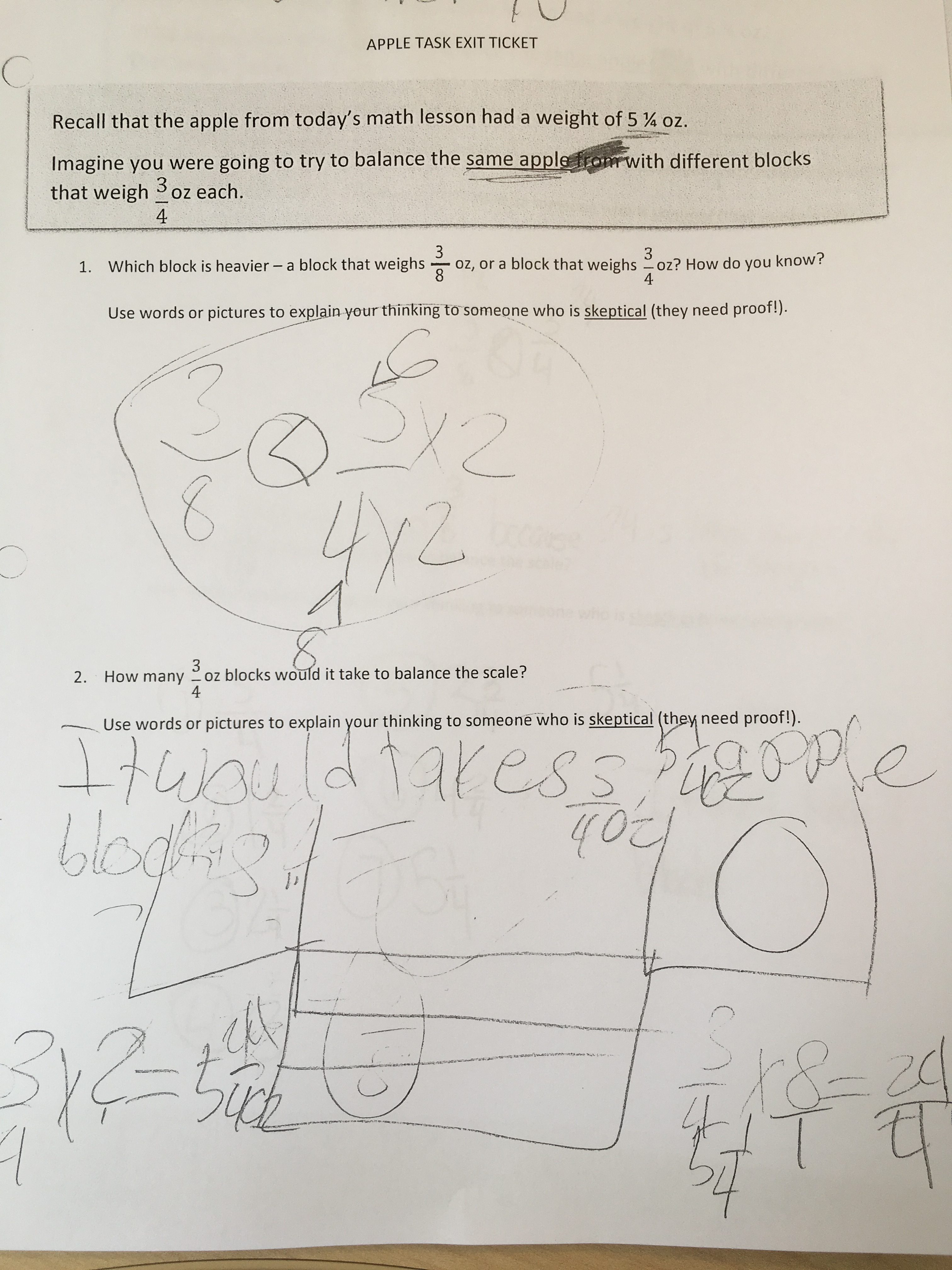
Afterward, we gave them exit tickets to see how they would solve a related problem – and to see how they were making sense of the fraction 3/8 as it relates to 1. Here are a few examples of student work :
All in all, this task was a great way to feel out students’ thinking about the relationships between addition, subtraction, multiplication, and division, and whether those relationships behave predictably with fractions. It was also a great way to peek into how students are marshaling procedures like finding a common denominator as steps to solving a problem, rather than as a procedure for it’s own sake. It’s clear that we have more work to do to build common understanding about some of these ideas, but I loved the opportunity we got to ask students to completely fly blind into material they’ve never ventured into before, and see what sense they made of it.