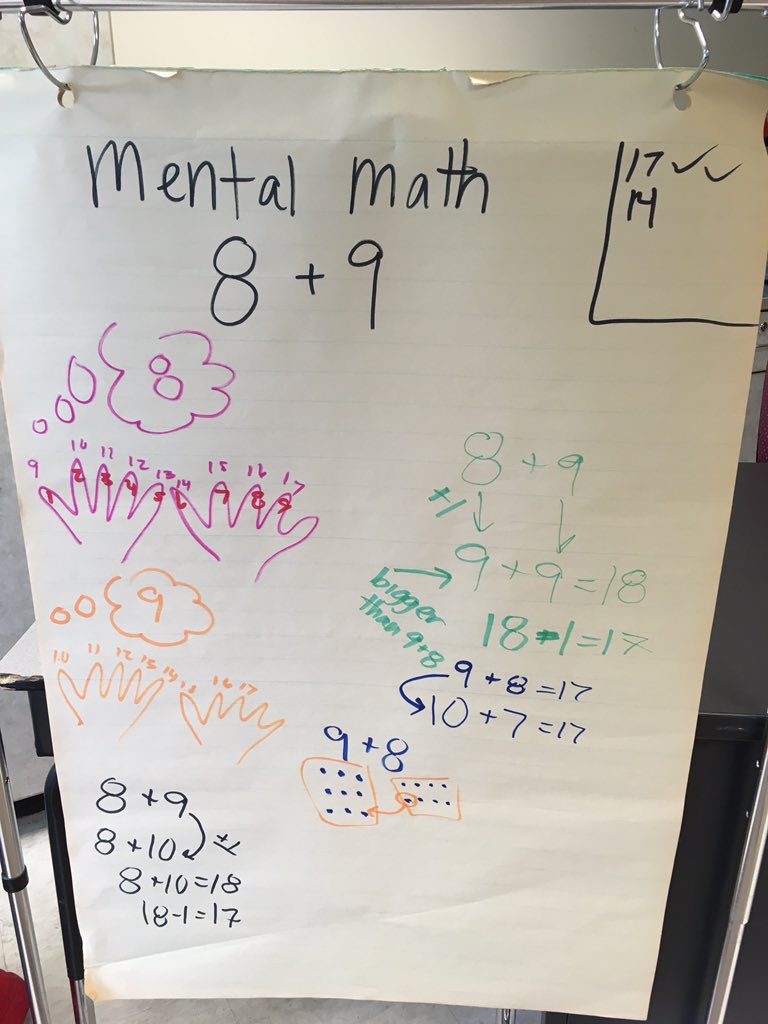Jessica is an undergraduate RA in the Sharpe Lab; she’s a rising second-year student majoring in Neuroscience. One of the joyful parts of this pilot semester on the TTP project has been getting to know each other as a research team from many places and backgrounds. In this post, Jessica reflects on one of the processes of our instrument development on the Teacher Pipeline Program (TPP) pilot this semester, in which we drew on published research findings and data to refine initial drafts of our interview protocols.
Early in our work as a research group, Dr. Sharpe recognized the need for us all to think together about the big ideas we wanted to dig into when interviewing students in the TTP project. Since Hanyi and I come from outside the education field, it was important for us to learn about the lives and experiences of teachers of color – a focus of the TPP project – in order to grow our own understanding. Dr. Sharpe learned about BlackMathTeachers.org, the research website of the Examining the Trajectories of Black Mathematics Teachers project (Frank et al., 2019).
This NSF-funded project used a combination of interviews, focus groups, and surveys to learn about the past and present experiences of Black mathematics teachers around the US, in order to inform future research and practice in schools, professional development, and teacher education. The website includes a wealth of research findings and both raw and thematically edited video data of the team’s interviews with retired math teachers.
In our second meeting as a group, we individually watched several video interview clips from the ‘college and path to teaching’ theme because of its relevance to the TTP project. Each video was short, only 5-15 minutes long, but packed full of experience and knowledge none of us had ever really fully run into. After watching, we discussed major ideas in what we heard, and then discussed how to adjust our own interview questions and tactics accordingly. Our main prerogative for watching these interviews was to allow us to think more critically about the interview protocols Dr. Sharpe had already developed. Mainly, we wanted to gauge whether or not they would be successful in helping us obtain the rich data we were searching for from the high school students in our study.
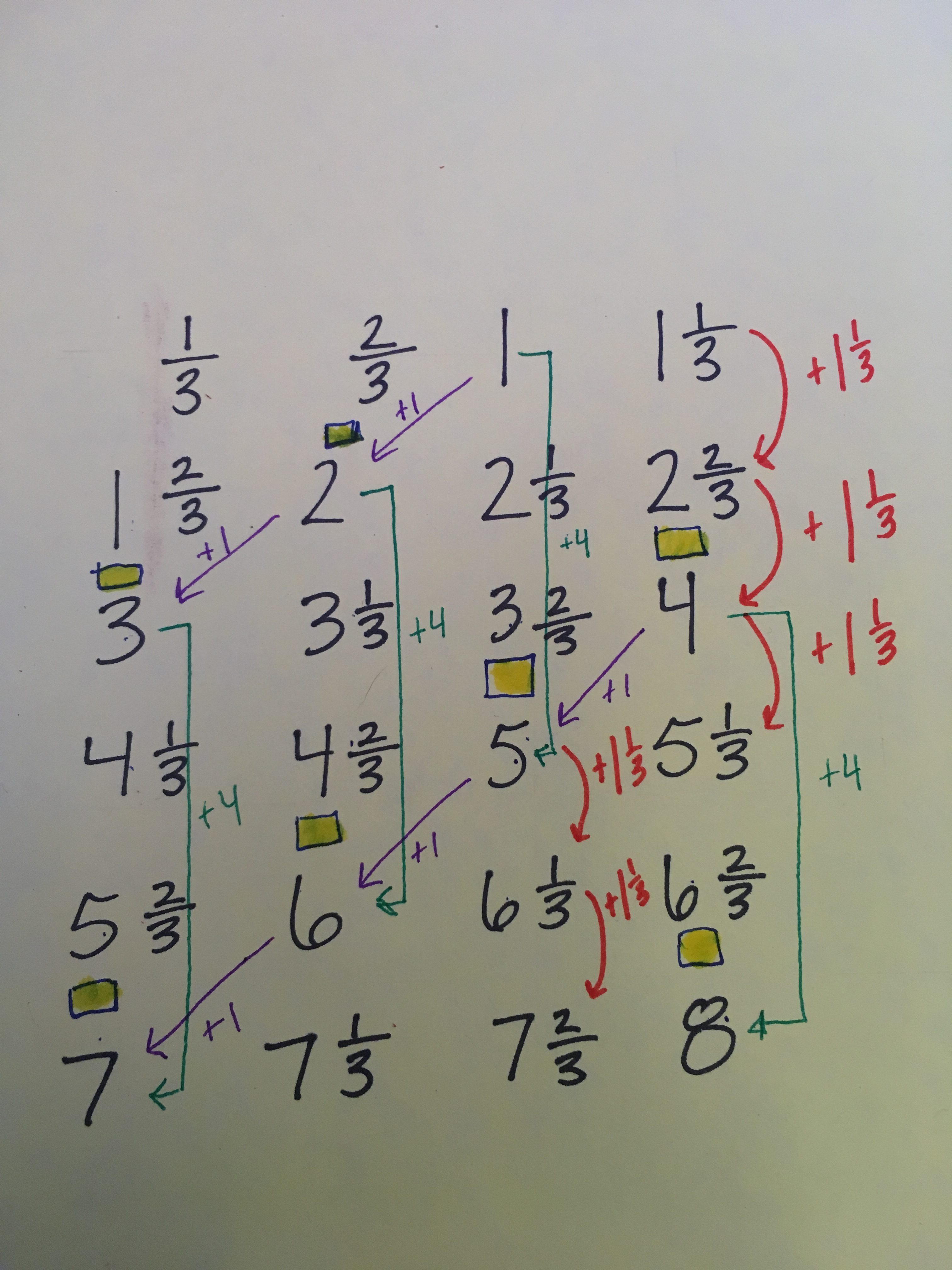
One of the keystone questions being asked in every interview was Why teaching? A version of this question was asked in every video interview we watched, and seemed to be one of the first questions asked that allowed each teacher to truly share their experience. Interestingly, the Black math teachers’ own experiences with the education system, particularly in college, seemed to be what developed their interests most. We took this information and applied it to our own interview questions. Some new perspectives we wanted to explore through our questions was what history of teaching the students had in their families (if any). We were also interested in any unusual challenging experiences the students might have gone through, and how they shaped their path to teaching. When talking with students of color, this question felt particularly important.
Another viewpoint we felt was important to touch base on in our interviews was the community each student felt they were surrounded by. We wanted to emphasize our consideration of their past and present school/ learning experience, in addition to their neighborhood or any teachers they felt connected to. Our hope was that not only would it help the students feel more comfortable and connected to their interviewer, but also get their perspective on the education system as it is. One of our goals through this research project was to encourage TTP students to stay in their communities as an educator. We asked students about how staying to teach in the area they grew up in would be beneficial for themselves and/or the students they would be teaching. This was a theme we revisited in focus groups and in our poetry mini-unit with 2nd grade students in mediated field experiences.
My own learning
Reflecting back on the process of revising our interview protocols, one thing I learned was the importance of allowing the interviewee to develop on their own thoughts without butting in, as it often led to some of the most important yet overlooked insights.
For instance, in her video interview, Dr. Sarah Keyton paused as she described the challenges of being a black female in the math field. After every long pause, she continued, eventually sharing how she felt incredibly intimidated at first.
This made me think about how at every crossroads or large change in my life, I’ve never thought twice about the authoritative figures in those settings. To me, every teacher was carefully labeled ‘The teacher’ in my head. Considering that the people in charge might be experiencing imposter syndrome or feel out of place isn’t a mindset I had ever experienced or thought about before.
This process also made me wonder how many of my teachers I’ve overlooked, simply because I didn’t think to ask about their own life experiences. I never took advantage of many of my teachers’ willingness to mentor on a deeper level. It’s easy to forget that many of my teachers wanted to do more than just teach. It takes a unique and wonderful individual to dedicate themselves to the art of teaching others, no matter the content.