Amanda is teaching 5th grade this semester at a local elementary school and recently got to enact the Final Lap task (created by Graham Fletcher) with her students. Note that Amanda changed the finishing times of the NASCAR cars to minutes, and limited the times to numbers in the hundredth place.
The instructional goal for this lesson was for students to compare decimals to hundredths by reasoning about their size and to recognize that comparisons are valid only when the decimals refer to the same whole. In lessons prior to this, students were introduced to decimals to tenths and hundredths and changing fractions into decimals/decimals into fractions. This lesson introduced students to comparing decimals. Another goal of mine was for students to understand how and why decimals are used. Some students were having difficulty understanding when we use decimals and the importance of them. Showing students a NASCAR race where the times of each car are given as decimals proves that decimals are used in everyday life, for various reasons, and assist us with tasks that must be completed. Therefore the instructional goals of this lesson were met because students compared real life race times (which helped them understand the usage of decimals) and ordered them from smallest to largest/first place to last place.
In the beginning of the lesson, the class created a notice and wonder chart about the NASCAR 3-Act Task video.

I anticipated that students would notice the numbers on the cars, which was good because that’s how we spoke about each of the cars (which got tricky when we added in the decimals we were working with. It was a lot of numbers to write and speak about). Also, I anticipated that a student would wonder, “why are we watching this video” and “who won the race”. This question – who won? – was the first one students asked, and the most to get the “me too!” symbol (sign language we use in class), which made it easy to come back to and highlight as our main question. During the creation of our chart I did not anticipate a notice about the decimals in the right-hand corner of the screen. Hearing this I was surprised because to be honest I did not catch this the first few times I watching the video by myself. When a student mentioned this as his notice I told him, “Speaking about decimals, I want everyone to keep everything they know about decimals in the front of their brain because it will come in handy.” I did not want to give away anything but I wanted the other students to start thinking about decimals and recalling prior knowledge/lessons.
Once we created a class notice and wonder chart, I asked the students what information/tools do we need to solve this problem. I anticipated the responses would be the lineup of cars and the amount of time each car finished the race. Instead, the only two responses I got were “more of the video” and “a picture of the finish line”.

This probed me to say, “Let’s say technology was not working and the announcers had to take notes of the race. What would we want to see and in their notes?”. I still got answers such as, “the car that won” and “description of which car won and how” but I also got the following response, “which cars finished the race” which lead to “how fast each car finished the race”. Although these weren’t the exact responses, they aligned with the information they needed to solve the problem and what I had to share with them.
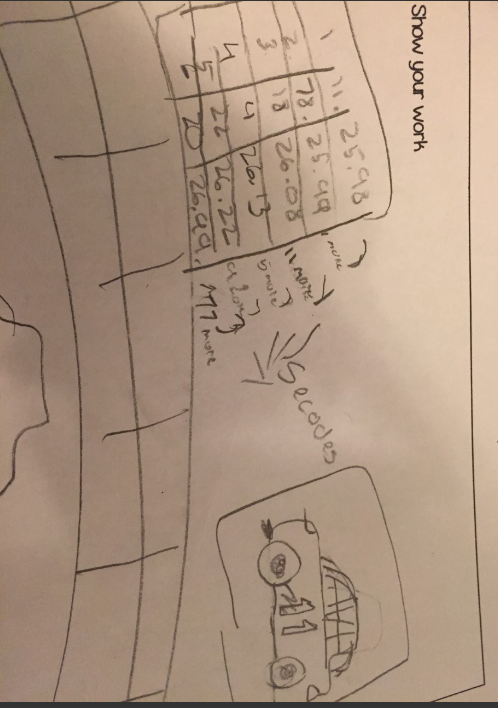
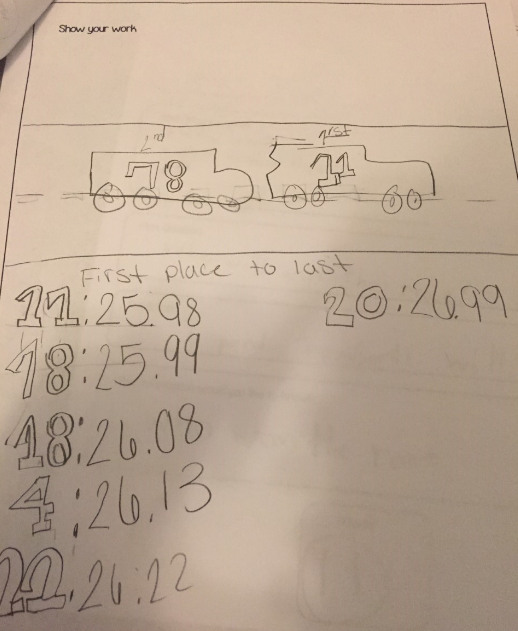
When I shared the information with the students I planned that some of them would know the answer right away. Predicting this, I told the students that if they knew the answer please be respectful and keep it in their minds, but if they wanted to share then they would have to use their whisper phones to let it out. During the enactment of the lesson there were students who were so excited they knew who won that they had to let it out so they used their whisper phones. This allowed students to not spoil the answer or persuade any of their peers’ thinking. Having students know the answer right away also led me to stating clear directions of, “proving your answer with work and using the decimals to do so” and extension questions that were as followed, “put the cars in order from 1st to 7th place”, “how many seconds did 1st place win by”, and “how many seconds did the 1st place car beat the 7th place car”.
Starting with the Notice and Wonder chart, I learned that it is a great activity for every single one of my students. Since this activity is “low floor, high ceiling,” students of all skill level can participate. For example, my student that rarely speaks in class due to language disconnect shared a notice about the color of the cars. Also, a student that is usually disengaged during the math block was the student that shared our wonder question, “Who won the race?”. I learned that if you give students the chance to show their knowledge from the very beginning of the lesson they will be more inclined to participate throughout the whole lesson/unit.
Also, I learned that my students are taught to think of math as a question and answer process. From the time that I stated the main question, most of the students were obsessed with getting the right answer. They asked, “what does this video have to do with the math were doing today?” and “Am I right?”. Even during independent work time, multiple students raised their hands just to ask, “Did I get the right answer?”. When I wouldn’t tell them or show them the final answer right away they got frustrated and questioned their work even though it was right. These reactions show me that my students are not regularly learning to value the process and instead focus on the correct answer or algorithm that will get them the “A” or “100 %”.
While sharing strategies, I learned that the students are most comfortable with thinking about whole numbers. Almost all of the students used strategies that sorted the times according to whole number then made a data table from smallest to largest or data table with the smallest whole numbers on top then the largest on the bottom and then wrote 1st, 2nd, 3rd,… next to the times. Also, while sharing their strategies, they called numbers to the left of the decimal whole numbers but they didn’t seem to have a name for the numbers for tenths and hundredths. Some students used these terms without probing, but most students caught on to tenths and hundredths after I went over the terms by showing them the following layout, “whole numbers. tenths hundredths”.
If I were to teach this lesson again, I would do a mini lesson prior to the 3 Act Task. This mini lesson would be on place values including decimals. I would have the students write any decimal they like (keeping it to no more than 3 numbers), write that decimal exactly how they would say it aloud, and then turn and share their number with a partner. This activity would allow for the students to have a productive struggle of what to call each place value. After a class discussion, I would show the students the actual decimal place value system. This would look like “whole numbers . tenths hundredths” or “hundreds tens ones . tenths hundredths”. Students could refer to this place value chart during the 3 Act Task and future decimal lessons. I would include this mini lesson prior to the 3 Act Task because when speaking about the times of each car students would say “26 point 23” or “the first/second number after the decimal”. It wasn’t only until I stopped the lesson to draw and explain the decimal place value system that they started using the language “tenths” and “hundredths”. Some students still fell back to the “26 point 23” or “first/second number after the decimal” but this tells me that they don’t fully understand what the tenths and hundredths represent. Therefore, with these specific students I would have to go deeper into exploring the decimal place value system. If I would have done the mini lesson I think students would understand tenths and hundredths which would have made the task easier to understand, contextualize, and more fluid.
Another change I would make is how I asked the students to show their work. I wish I would have asked the students at first to order them from 1st to 7th place instead of making that an extension problem. I would do this because it would force students to interact with the decimals from the beginning and not just use mental math to figure out who won. Also it would give me more time to focus on strategies because I wouldn’t have to go up to each student who finished and ask them the first extension question.
Based on how the lesson what I would conduct a number talk and have students compare 25.3 and 25.29. This question was my exit ticket, but I ran out of time to hand it out. I would choose this specific problem because I want to see which students understand the place values of tenths and hundredths, and whether they can compare the number of digits with the value of each digit. Also, it would encourage them to recall the names of the place values and use them to describe their thinking.