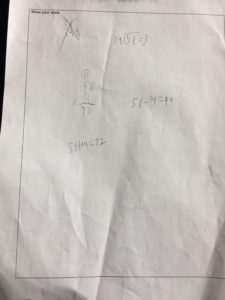This reflection comes from Connor, who enacted @gfletchy‘s task Array-bow of Colors with 5th graders this past spring.
My instructional goal for this lesson was to have students make the connection between repeated addition and multiplication while solving a problem. Students worked towards this instructional goal in the strategies that they used to solve the problem when working independently and when sharing their answers. I chose the order of responses so that the students would first see how to multiply by breaking the numbers down. Next, they saw how to solve the problem using the traditional algorithm of multiplication. To connect the two multiplication strategies to repeated addition, I had a student discuss how they skip counted to find the answer. The student did not have the opportunity to finish the skip counting, but as a class we discussed how to skip count, which numbers to use, and when to stop.
The Three Act Task started with the students watching the first video. The students noticed many things that I did not notice when I watched the video. For example, one student described that as the skittles were poured into the jar they made a pattern. One other student noticed that the skittles were poured into the jar until it was filled. To extend off of this, and to clarify for the rest of the class, I asked the student where the jar was filled to (to the very top, or to some other point in the jar). I realized after teaching the Three Act Task that I forgot to have students participate in a turn and talk with the person or people sitting next to them. If I taught this lesson again, I would make sure to have students have an opportunity to share their responses with their peers.
After writing down their notices, the students watched the video again and wrote down any wonders that they had. The students participated in a turn and talk with the person or people sitting next to them. The responses that I received were all relevant to the central question. For example, one student asked, “How many wrappers were left over?” Another student asked, “How many bags did he put in the jar?” I was able to make a connection between these two questions, and how they both asked sort of the same thing. The students were able to come up with the central question as one of the wonders. For this three act task, the central question was, “How many skittles were in the jar?”
After writing down the notices and wonders from all the students, I introduced the estimation portion of the lesson. The students were all able to write down a low and high estimate, but some of their estimates could have been better. For example, one student wrote his low estimate as 1. While this is correct, there is a better estimate that he could have written down. When practicing for this lesson, I tried to think of a way to help the students make better estimates. In the video of Graham teaching his Three Act Task, he told the students to, “be brave” when they were making their estimates. If I taught this lesson again, I would try to think of a way to help the students make estimates that were ambitious, but also based on what they already knew.
To move forward from the estimation to solving the problem, I first asked the students how confident they felt about their estimates. Then I asked the students what information they would need to help them make more confident. I phrased the question like this, because even though they are answering the question, how many skittles will it take to fill the jar? The answer is an estimate based on the assumption that there are 14 skittles in each of the bags. The students used the number 14 when solving the problem, but in reality, there were different amounts of skittles in each of the bags. I asked the question to the whole class, but only one or two students raised their hands. To promote more participation, I asked the students to participate in a turn and talk with the person or people sitting next to them. When the class came back together, the students explained that they would need the number of skittles in the bags, and how many bags were used to fill the jar. When giving the students the information, I was careful to state that there were 14 skittles in this bag (the bag that was shown in the picture).
The students also correctly identified that they would need to know how many packages of skittles were used to fill the jar. First I showed the students a picture of a pile of all of the packages and asked them to estimate how many there were. When sharing their responses, the students did not appear to have used a strategy to estimate, and instead just took a guess. To finish this portion of the lesson, I showed the students how many packages were actually used (58). The students began to work on answering the question.
When I circulated around to observe what strategies the students were using, I noticed that there were three main ones.
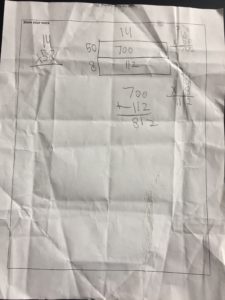
The first, and most common strategy that students used was to set up a vertical multiplication problem with one number on top of the other. While many students were able to set up the problem correctly, not many were able to get the correct answer. After teaching my lesson, I found out that the students have not learned how to do double digit multiplication using the traditional algorithm. In their work, the students would multiply one digit by the other two (for example in 58 x 14 the students would multiply the 4 by the 8 and 5), but would not finish the problem by multiplying the other digits together. In addition, one of the other challenges that students had with using the traditional algorithm was that they had trouble lining up the digits to get a correct answer. Even if the students multiplied the digits correctly, when figuring out their answer, the students would not line up the numbers correctly, and as a result would not get the right answer. To help students understand how to use the traditional algorithm correctly, when sharing answers, I made sure to talk about the place value of each of the digits in the number. I also walked the students through the multiplication process and how the algorithm was used in this problem. My teacher told me that the students will be learning how to use the traditional algorithm soon, because it is on the state test in the beginning of May.
Another common strategy that students used to help them solve the problem was to break one of the numbers up and then to multiply it by the other number. For example, when implementing this strategy, one student broke 58 into 50 and 8. Then he divided each number by 14 and added the products. The student got the correct answer using this strategy.
One last strategy that some students used was skip counting. The students used this strategy most often to add 14 together 58 times. When sharing this strategy with the students, one identified that while this strategy works, it takes a long time, and can be hard to add together. Based on this, I asked the students if skip counting and repeated addition would only work with 14. The students replied that they could use the same strategy for 58, but also explained to me that it is harder for them to add 58 together 14 times. I tried to connect the repeated addition strategy that was used to the two multiplication strategies by reviewing one of the claims that was made in the mental math. In the mental math, one student explained that repeated addition was a longer way of doing the multiplication. To review that in my lesson, I asked the students what numbers they used in the addition sentence, and how this connected to the multiplication that was done earlier. The students were able to identify the connection that they discovered in the mental math.
At the end of the lesson, I revealed the answer to the students. They were confused as to why the answer that Graham Fletchy got was different from their answer. To help them understand why, I offered up a situation where two of the students have the same brand, size and type of chips. I asked the students if each of the bags would have the same number of chips. Some students still appeared confused by this situation, but others began to understand what I was saying. One student explained that if they counted to make sure that every bag of chips had the same number of chips in it, the factories would not make that many bags each day. Transitioning back to the lesson, I asked the students how they could connect the chip scenario to the skittles. One student raised her hand and said that just like the bags of chips, each package of skittles would not have the same amount of skittles in it. Going off of this, I explained that we only knew how many skittles were in the first package, and not how many were in each of the other bags.
To finish my lesson, I gave the students an exit ticket, asking them to determine how many skittles were in a case of skittles that was pictured on their exit ticket. The students were given the number of skittles in one package, and how many packages were included in the case. From this, the students solved the problem again. One of the changes that I saw between the work they did in the lesson and the work they did on the exit ticket, is that more students used the second strategy on the exit ticket. Many of the students broke up the number 36 into 30 and 6, then tried to do the multiplication. However, some students still seemed stuck when they went to multiply 56 x 30.
From this lesson, I learned that my students can apply previous strategies that they have learned to new situations. In this lesson, I was not teaching the students any new strategies, or ways to solve a problem. Rather, I was seeing how well they can apply strategies and techniques that they have learned already. The students proved they were able to do this by using the multiplication strategy that my host teacher taught them earlier in the year, and by relying on their knowledge of skip counting.
I also learned from this lesson that my students need some strategies to help them make more educated estimates. In the lesson, the students first made estimates about how many skittles they thought would fill up the jar. The students’ estimates were not always realistic, and many of the students put estimates that were safe. For example, when asked to write a low estimate of how many skittles would fill up the jar, many students wrote down 1. While this is correct, there were other, higher numbers that could have been used that were more ambitious. The students next used estimation when trying to figure out how many packages of skittles were used to fill up the jar. The students guessed estimates that again did not seem realistic. When asked how they came up with their estimates, none of the students had a strategy that they used. Instead, it became clear to me that the students were just guessing how many packages were used.
If I were to teach this lesson again, I would change the way that I wrote down the notices and wonders. In my lesson, I set up two pieces of paper in the back of the room where I wrote down the notices and wonders. However, because of the placement of the papers that I was writing on, the students had to turn around in their seats to look at me. This led to many students not looking at me when I was teaching, and students having to turn around every time that I wanted to talk to them. One other thing that I would change about the notices and wonders section, is that I would write them neater, and also larger. I noticed after writing down the notices is that they were very small. I tried to write larger when writing down the wonders, but they could have been neater. One of the problems that I ran into, was that I did not want to turn my back on the students for too long.
If I were to teach this lesson again, I would also try to ask more questions about the strategies that students used. While I asked questions about the strategy that was used, looking back, I should have started with more basic questions like, “How did you know to multiply 58 and 14 together?” This would have allowed every student to understand the strategy before moving on to more complicated questions that would establish connections between the strategies.
If I were to teach this lesson again, I would also ask the students to draw a picture of the problem. This was not a central focus of my lesson, so I did not emphasize it as much as I should have. Creating a visual representation of a problem is important because it helps students make sense of the problem. I decided not to push the students to draw a picture of the problem because it was not a strategy that I saw the students using. I did not know how to introduce this strategy, or if it was something that I should introduce. Instead, I decided to focus more on the strategies that I saw students using.
Based on this lesson, the next choral count, mental math, or Three Act Task that I taught would be focused on connecting a picture of a problem to repeated addition and multiplication. After the sequence of lessons that I taught, I am confident that students understand the connection between repeated addition and multiplication. In my next lesson, I would try to extend that connection to creating a visual representation of the picture. This would help students make sense of the problem that they were trying to solve, as well as seeing how repeated addition and multiplication are used, and where each of the numbers in the number sentences comes from.