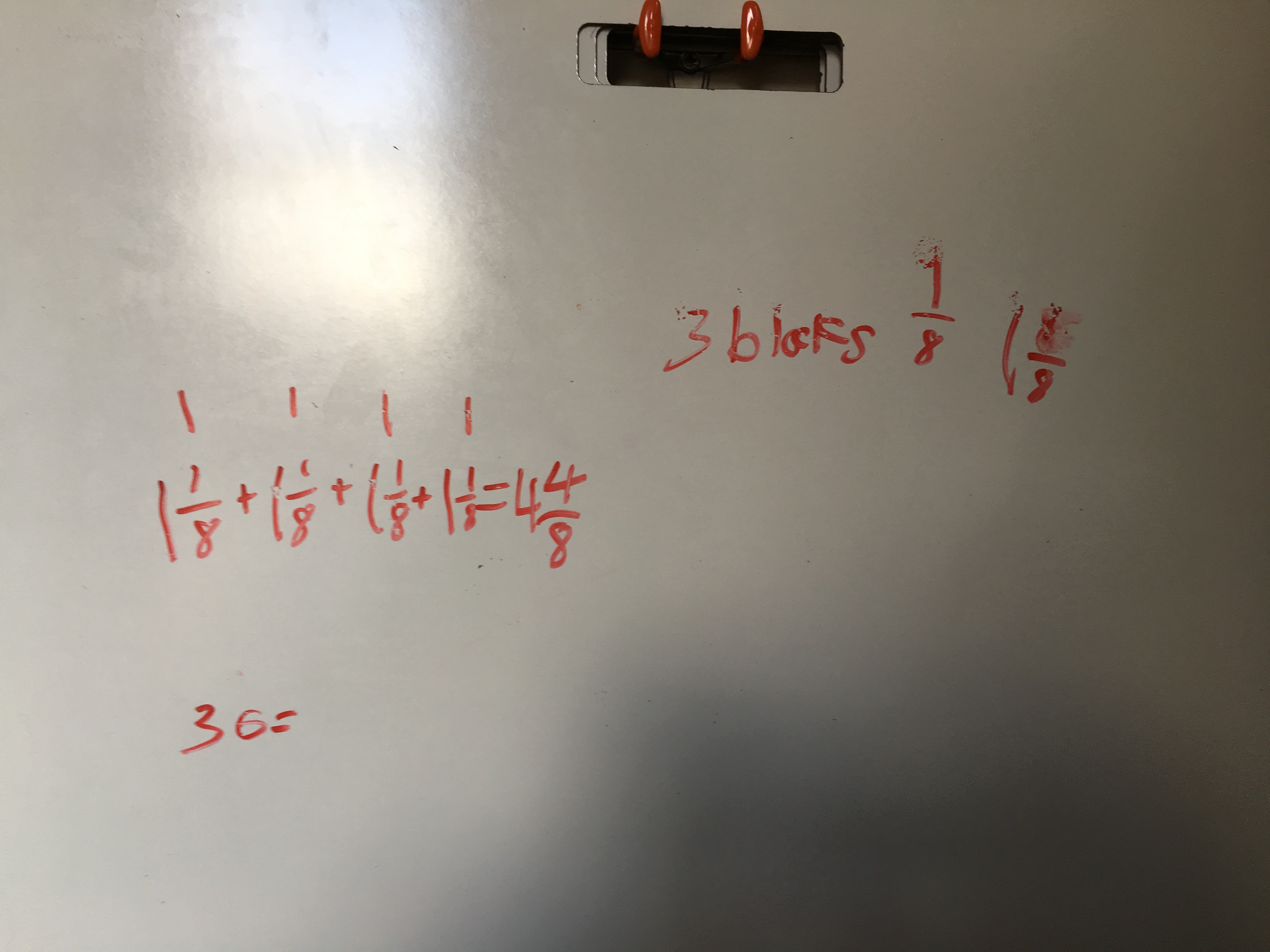So far in summer school, we’ve been working on sociomathematical goals: getting students accustomed to routines and procedures for sharing their thinking in pairs, in written work, and in whole-group dicussions. Mathematically, the activities and lessons we’ve used to develop these goals have been focused on multiplication and the relationship between skip counting, grouping, and array models of multiplication. This has helped us identify students who need extra support (since multiplication isn’t ‘new’ content for 3rd grade) while also being a slightly more approachable area to start number talks with.
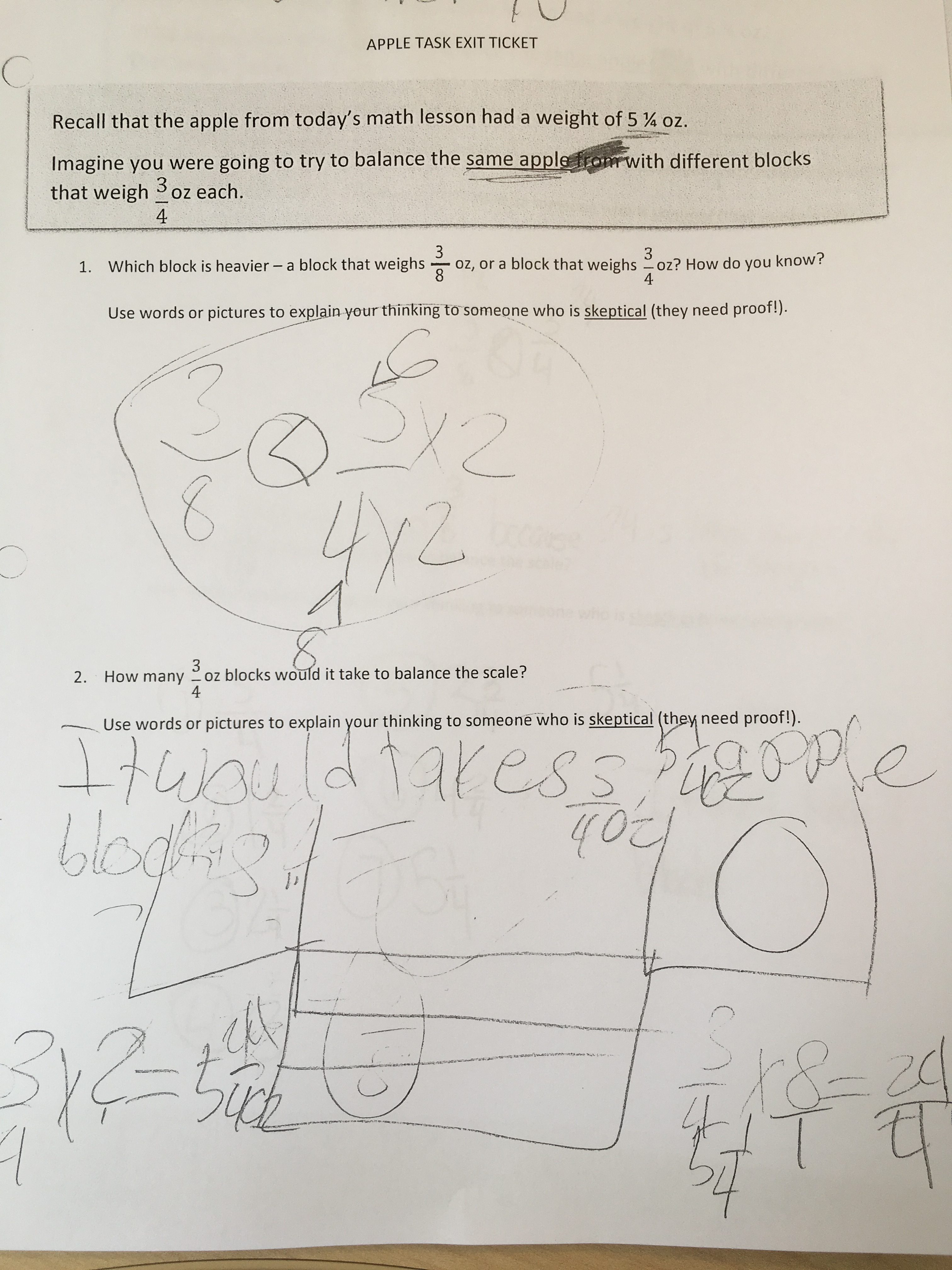
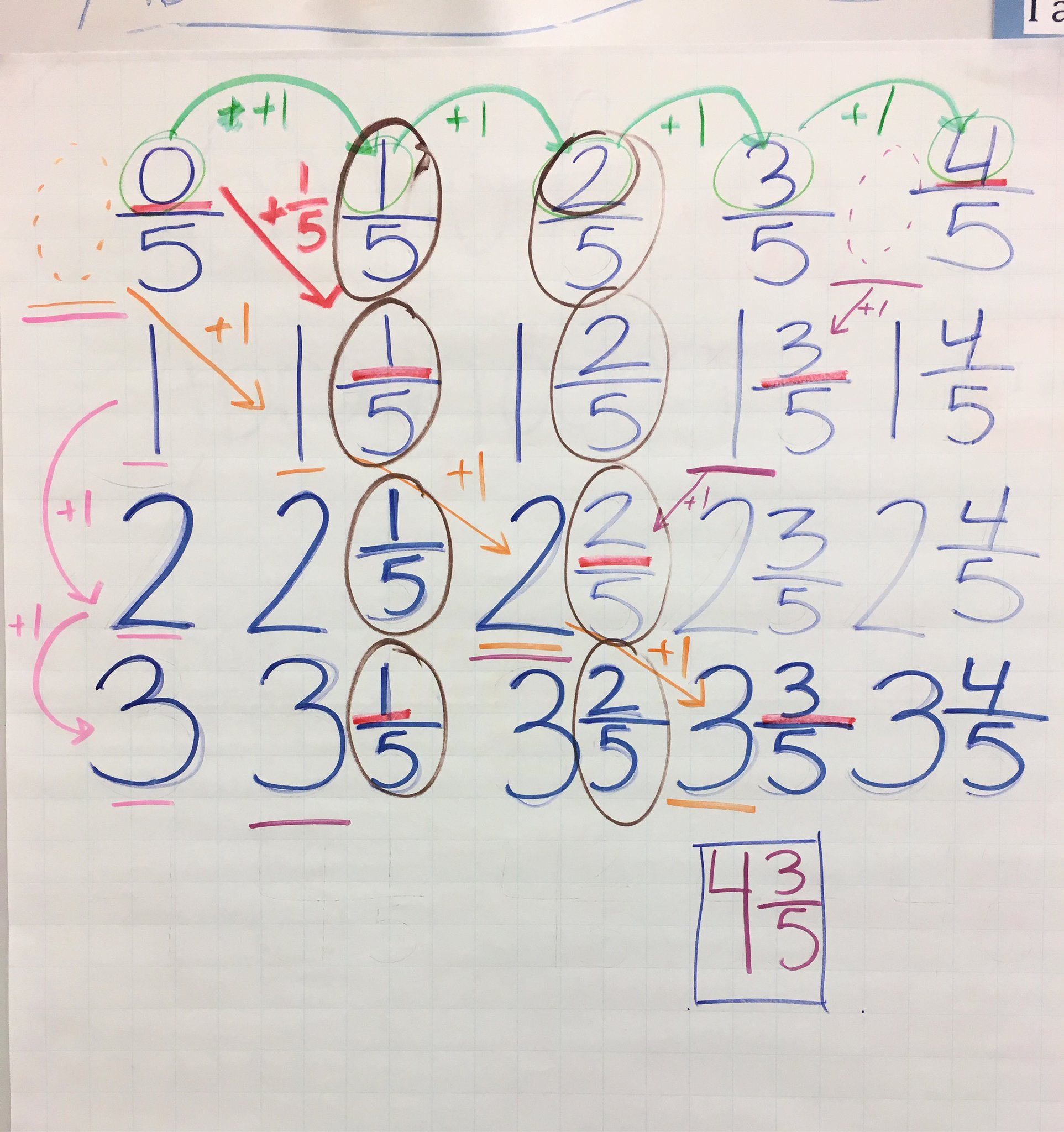
Last week in our classroom, we began work on the content standards that gave our 3rd graders the most trouble on the end-of-year assessments administered by the state and by the school: fractions. Specifically, these students need additional support in understanding what a fraction represents, how fractions can be represented on linear models, and how fractions can be different and yet equivalent. To start this work last week, we began by creating Fraction Kits based on the insight and advice of Marilyn Burns, whose book has been an excellent tool for lesson planning and mapping the mathematical terrain we need to help students explore this summer.
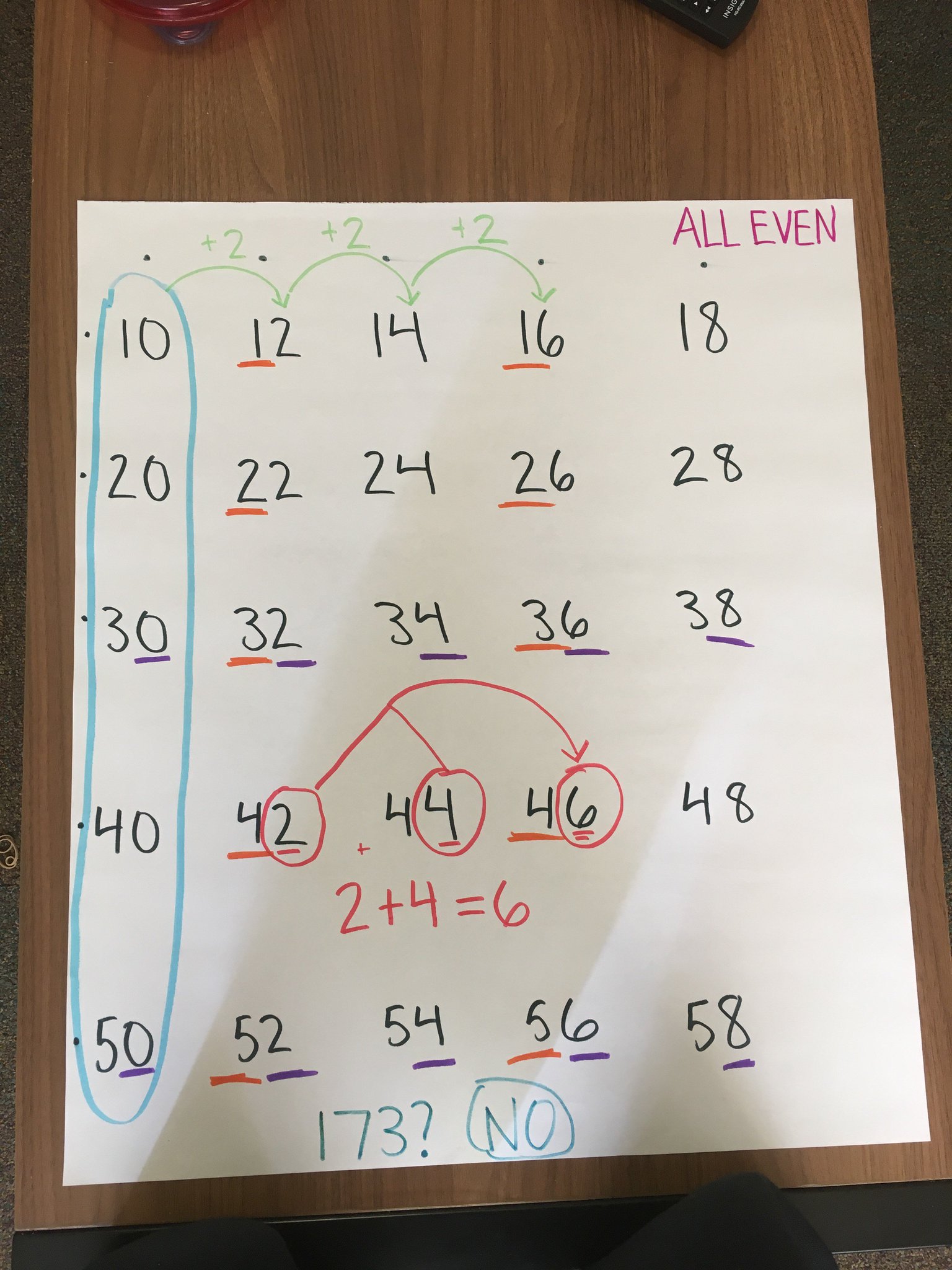
Monday and Tuesday we spent time counting collections, and observing how students were grouping objects.
Wednesday we began math class with a mental math number talk, solving and discussing strategies for 6×7. I was glad to see that students were willing to persist even if they didn’t “just know it” from memory – they were willing to think and find a means of figuring out the problem.

After our number talk, students returned to their seats where each received a set of pre-cut strips of construction paper and a large envelope cut from similar construction paper. They wrote their names on the envelopes and tucked them inside their desks.
Next we went through the process of folding our strips. For each strip, we:
-folded (I first modeled how to fold them)
-predicted how many sections there would be before opening to see
-decided as a group how we might then label each section
-waited for each student to fold, unfold, label each section, and label the back of each section with initials.
Once every student had their fraction pieces folded, labeled, and affixed with initials, we passed out scissors and got them cutting.
Why do, We do, You do?
I want to note that ordinarily, I steer away from “I do, we do, you do” type teaching. However, for creating fraction kits, I modeled first, together we decided how we might name/label, and then asked students to do it on their own. The reason I thought modeling and duplication was fitting in this instance is that our goal was for students to create tools that they could then use to explore fraction relationships. If their kits weren’t created correctly (and some weren’t: a couple students mis-folded and needed help to tape or re-cut later), they might develop some sneaky misconceptions about how much bigger 1/4 was than 1/8, etc.
So why not pre-cut the strips?
Giving the students a chance to fold and cut did elicit some students’ initial ideas about what those weird hyroglyphs called fractions might mean: many students were catching on to the pattern that “8 pieces mean each is called 1/8” and so on. Folding their own strips was also a useful opportunity for them to consider what happens when you take a half and fold it in half. For instance, when we folded the strip into 1/4ths, many students predicted that we would unfold the strip to find 6, 8, or 10 segments, rather than 4. Similar guesses of 10, 15, and 20 came out when we folded the strip into 1/8ths by folding it in half, half again, and half again.
Wrapping up
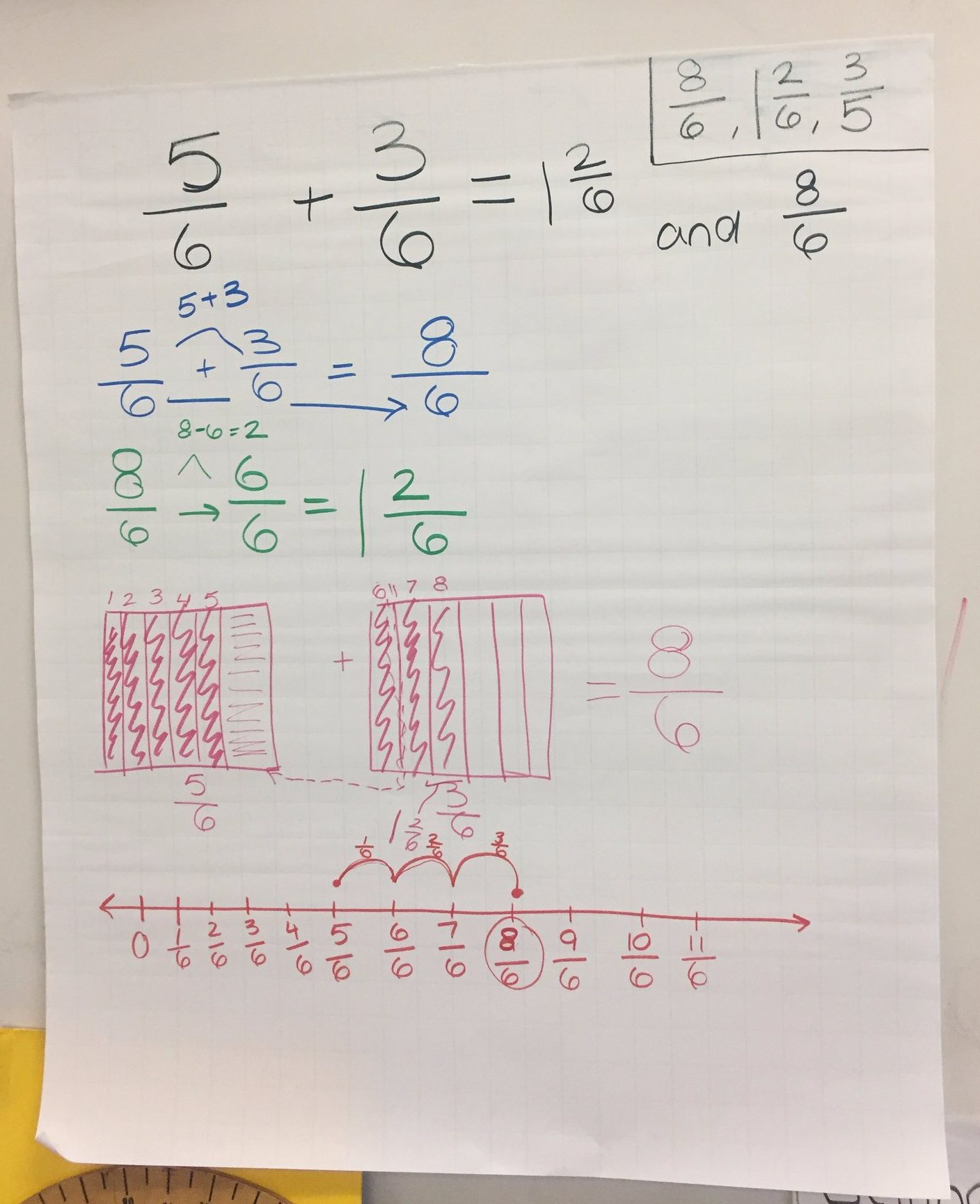
Because we opened with a number talk, we only had time to get the strips cut, labeled, and put away on Wednesday. But we did close by asking students to see if they saw any “matches” between strips of different size. This got a few initial ideas out on the table (or in our case, the smart board): two 1/4th sized pieces was the same as one 1/2. Similarly, two 1/8 sized pieces was the same size as 1/4.
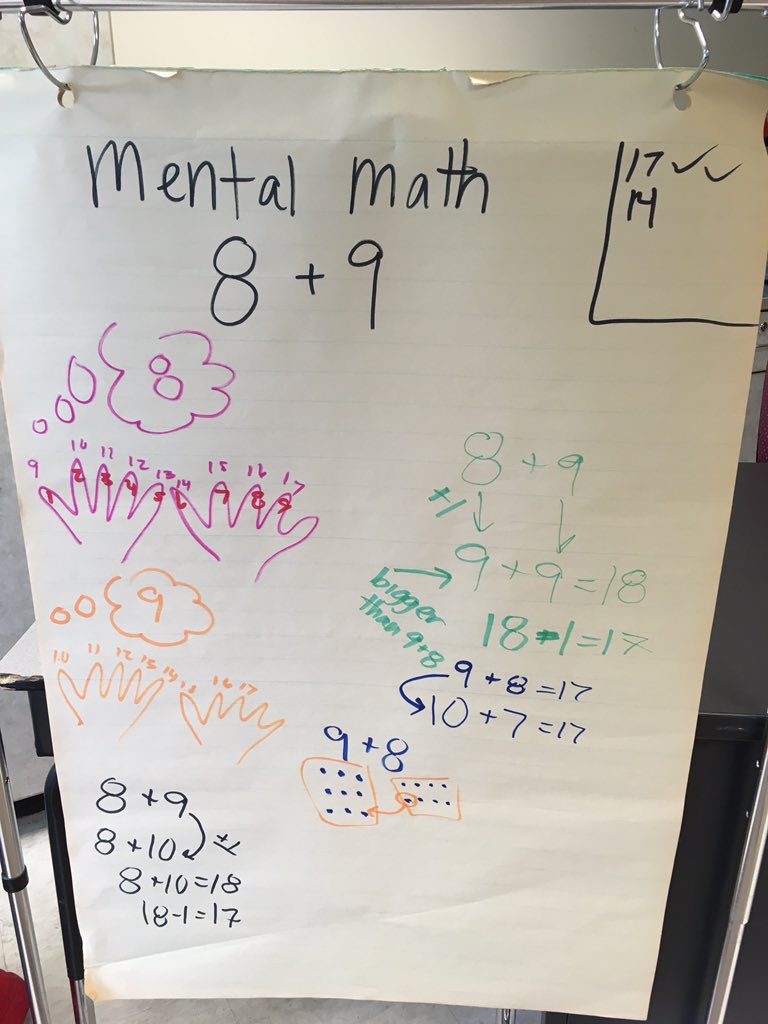








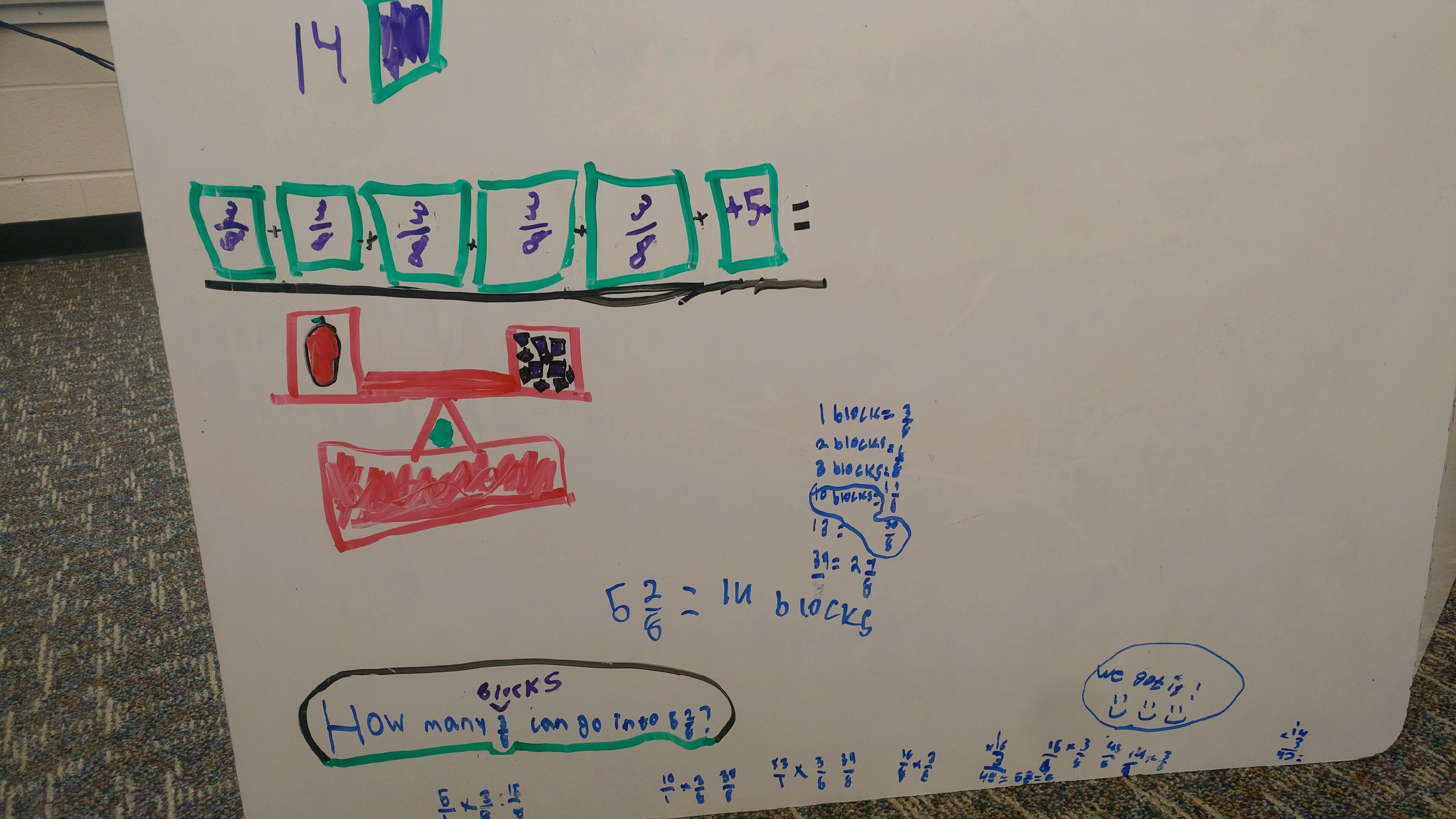
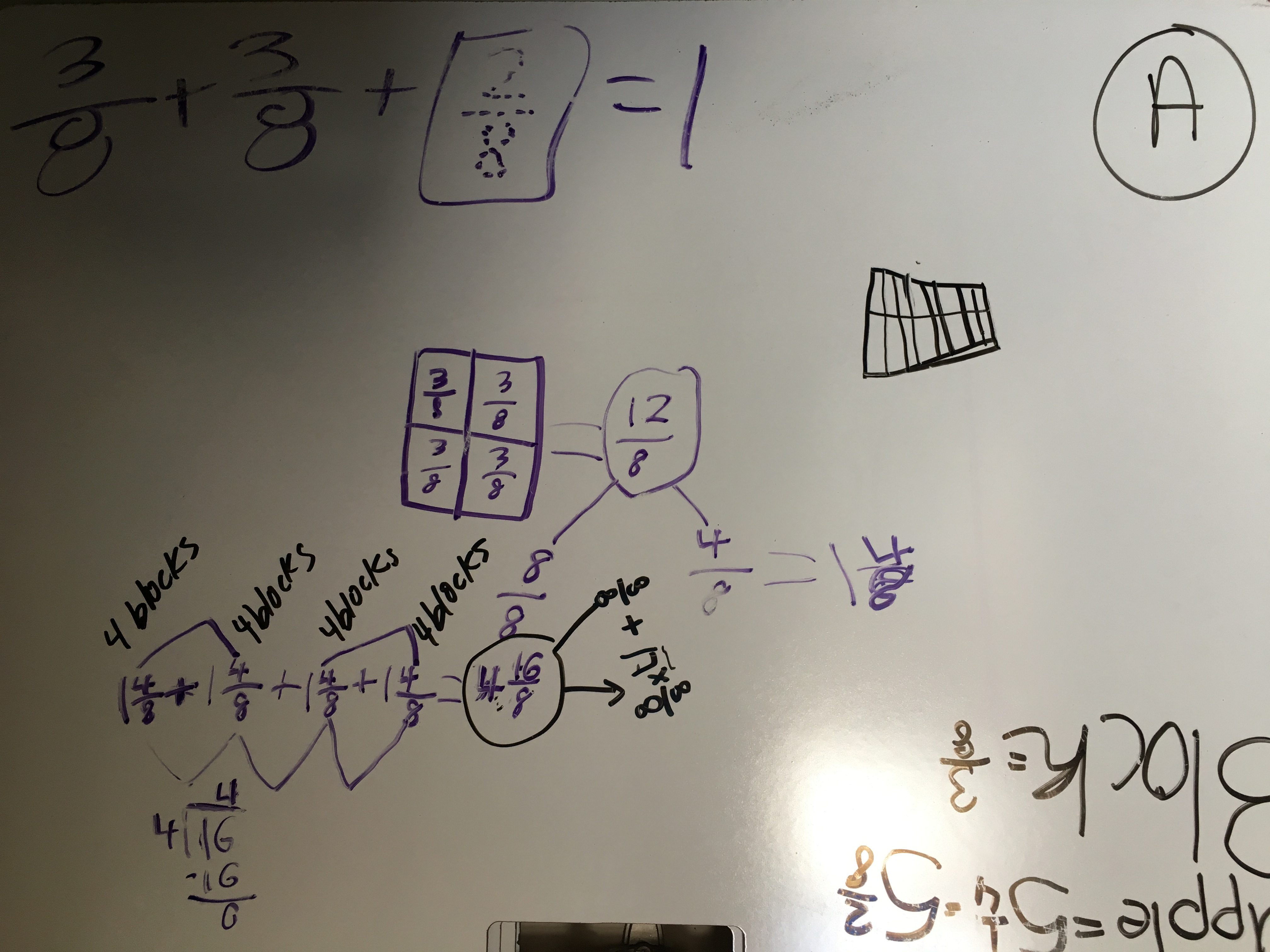 I LOVED this strategy. This group was led by two students in particular whose really wanted to find a combination of blocks that would add up to an easy ‘split.’ So they settled on 4 blocks, since 4 groups of 3/8 makes 12/8, which would only need 1/2 an ounce to get to the next whole. They knew, then, that two groups of 4 blocks would ‘make up’ the next whole.
I LOVED this strategy. This group was led by two students in particular whose really wanted to find a combination of blocks that would add up to an easy ‘split.’ So they settled on 4 blocks, since 4 groups of 3/8 makes 12/8, which would only need 1/2 an ounce to get to the next whole. They knew, then, that two groups of 4 blocks would ‘make up’ the next whole.