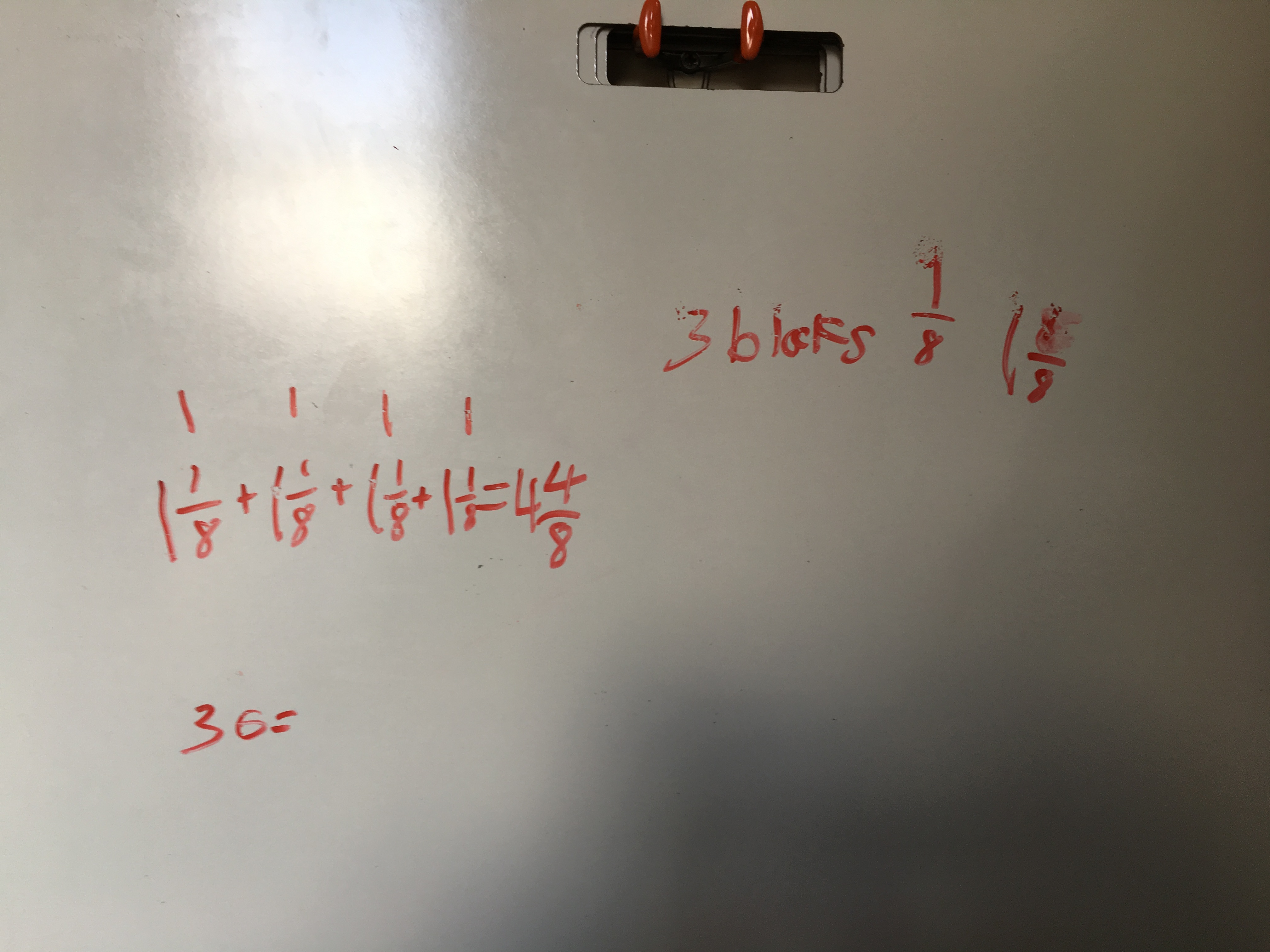Field Lesson Reflection

Exploring fraction operations with Choral Counts

I think sometimes it’s easy to see Choral Counts for their glitter, and miss their substance. People quickly fall in love with them because they’re fun, engaging, interesting, and they get kids talking about math. And these are great reasons to love and choral counts!  Beyond all this fun, though, choral counts (and the representations they produce) can support students to investigate really critical concepts – even in the older grades.

Yesterday I worked with some 5th grade teachers to plan some choral counts they can use in their current unit, which is all about fraction multiplication and division – specifically, division of whole numbers by fractions, and vice versa. Can choral counts support students in this unit? Absolutely.

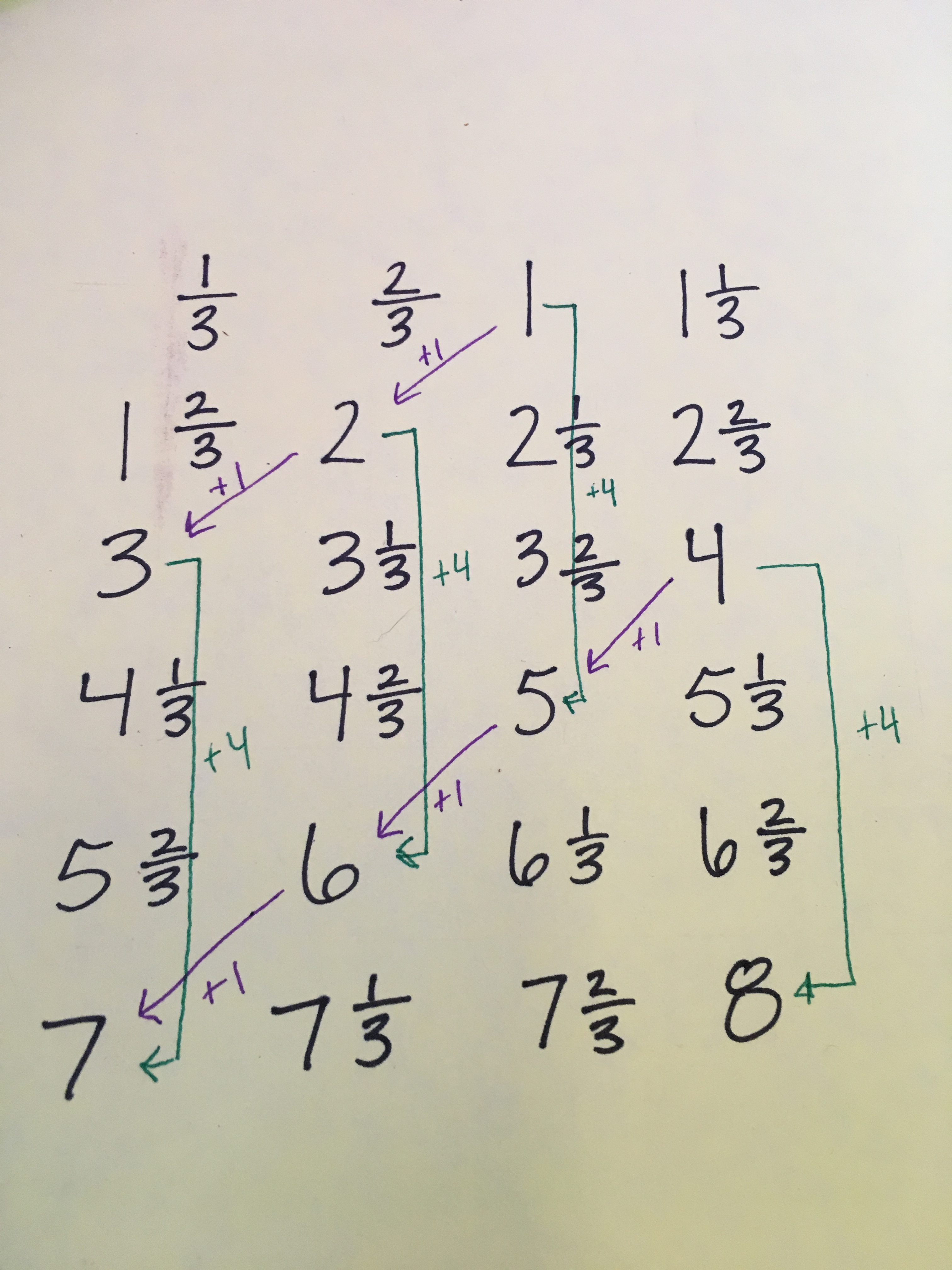
Check out this count we went through yesterday. We counted up by 1/3, starting at 1/3, using rows 4 across. I specifically chose to use rows of 4 in this count to make it “offset” in a way that would create some neat patterns. We found lots! What patterns do you see in this count?

Here are some we found:

  • The down-left diagonals increase by 1.
  • Three hops ‘down’ the column is an increase of 4 (this is especially apparent for the whole numbers, so that’s where I marked them.)

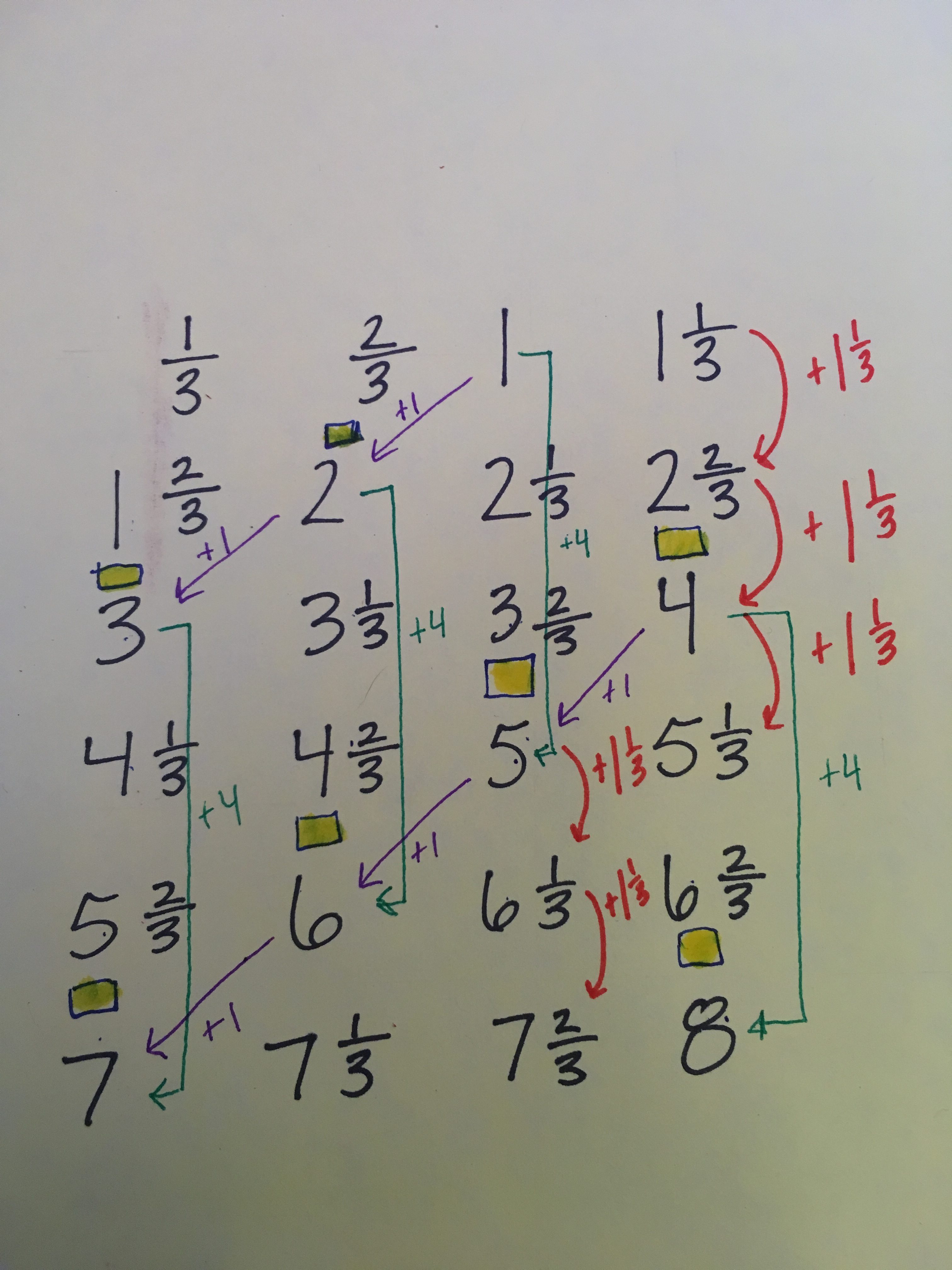
Each hop ‘down’ a column is an increase of 1 1/3.

  • There are some “missing” whole numbers in each column: for instance, in the third column, there’s no 4. In the fourth column, there’s no 7.

By drawing a little box where all the missing numbers are, another interesting pattern emerges…

Ok ok ok, we could do this all day. But what about exploring fraction multiplication and division with this count? 

Consider posing the problem 8 ÷ 1/3. How would you solve this problem mentally? How might 5th graders?

Now, try using the finished count to solve this problem.

.

.

.

(Think about it on your own before you scroll down.)

.

.

.

One way of thinking about 8 ÷ 1/3 is, “how many 1/3 counts does it take to get to 8?” So we can get the solution by counting our ‘hops’ in the count. Because we didn’t start at 0, we count the numbers, not the hops.

Something that struck us in our PD meeting yesterday was that this is a nice way for students to confront their (totally reasonable) preconception that dividing always ‘makes something smaller.’ But how can we hammer that home?

Consider adding more problems in a string – building larger divisors. How could you use the count to figure out
8 ÷ 2/3? Students first have to figure out what 2/3 looks like. Can you build 2/3 by grouping 1/3’s? Sure! So how would that help us solve the problem? Count the hops again – only this time, we’re counting 2 hops at a time.

Something we’d want students to really be firm on: 2/3 is larger than 1/3. It’s a larger divisor.

So, let’s check out one last problem:  8 ÷ 4/3. [First: we want students to make a mental note. 4/3 is larger than 1/3 and 2/3.] Woah woah woah – dividing by an improper fraction?? Why not? Again, students need to first figure out where 4/3 appears in the count: can you build 4/3 by grouping 1/3’s? sure!  So using the same process we did above, we build a larger divisor and count those hops.

So now, let’s check out this string of problems and solutions that we’ve created. What might students notice? What big ideas might this string help them to make sense of? What questions might you as a teacher pose to students to get them thinking about those big ideas?

 

 

 

 

 

 

 

 

 

 

 

 

 

So, in sum, here are some big concepts you might explore in a choral count like this one:

  • Fractions can be decomposed into unit fractions – and unit fractions can be grouped together into larger chunks – even into chunks larger than 1! This is actually a 4th grade standard, but it’s very likely that 5th grade students need more opportunities to see this concept in action.
  • Dividing something relatively big by something smaller means fitting small things into something big. So we shouldn’t automatically expect the quotient to be a smaller number than the dividend. This is essentially applying a 3rd-grade understanding of the meaning of division to fractions – and thereby arriving at a key 5th grade standard.
  • The larger the divisor is, the bigger the thing is we’re trying to ‘fit’  into the dividend. A related idea is that the closer the divisor is to 1, the closer the quotient will be to the dividend.

Have you used choral counts in your classroom to explore and model similar concepts? Tell me about it in the comments – I’d love to hear!

Counting Collections: not ‘too young’ for 3rd graders

The students in our 3rd grade summer school classroom have many strengths. They work well with partners, they can commit to a strategy until they have finished a problem, and they are curious and excited to solve problems.

The third grade standards outline that third graders should be developing algebraic reasoning to help them relate addition to multiplication and division, and that they should be developing conceptual understanding of fractional parts of wholes, modeled in sets, area models, and linear models. While some of these goals still seem a bit far from our current students, we are working to approach these goals in stride by building on what they are already comfortable and confident with: counting.

For that reason, we spent time Monday and Tuesday doing some counting activities: Counting Collections and Choral Counting.

Counting Collections

I learned about Counting Collections as an instructional routine from the good folks at TEDD.org, whose work in teacher education pedagogies has been foundational for my own work as a teacher educator at Syracuse University.

Counting collections is an engaging, hands-on activity that packs a lot of ‘punch’ mathematically. Students work in pairs and are given a collection of objects to count, and some kind of sorting tool.  They devise a way to count their collection, follow through with their plan, then represent their thinking on paper using words, pictures, and/or numbers. This activity is great for getting a view into how a student relates counting to grouping and multiplying. For instance, many students in our class will group objects into the sorting tool, but then proceed to count them by 1s.  Others sort, then skip count. Others will sort them out, count up the groups, then multiply to find the final answer.

Collections I use: rocks, vase stones, marbles, cotton balls, multilink cubes, 1″ wooden cubes, 1cm plastic cubes, pennies, red/yellow counters, plastic drinking straws, small cloth hair bands that come in packs of 200 or more [The dollar store is great!!]. Most of the collections are around or just over 100.

Sorting tools: egg cartons, small dixie cups, 8oz styrofoam cups, 6″ styrofoam plates, rubber bands, large egg cartons (The kind that hold 36 eggs).

The routine:

1. Expectations!

We start by outlining (and on subsequent days, reviewing) expectations for student work during a counting collections activity:

  • Respect your partner by taking turns, being kind, trying to help, being fair
  • Respect the materials by taking care of them, keeping them clean, putting them away at the end like you found them
  • Listen and Explain to understand – don’t stop until you both agree and understand on how you’re sorting, organizing, grouping, counting
  • Help your teachers understand your thinking by explaining with words, by writing neatly, by using words, numbers, and pictures to show how you grouped and counted

2. Find a partner, find a seat!

Students get with a partner and move to a place on the floor where they have some space to themselves. I recommend not working at a desk, because small things (pennies, marbles) will roll off or slip through cracks.

3. Pass out collections.

Certain collections will become extra treasured (in our case, the marbles), so emphasize that you’re passing them out randomly, but that each student will get opportunities to count new collections each time. Something we haven’t done that I plan to implement: adding a “log sheet” index card to each collection baggie, so that each pair of students can write their names to keep track of which they’ve counted and which they haven’t.

4. Get counting and recording.

As students work, the teachers move around the room, asking students to explain how they’re grouping and why, and how they’re using those groups to help them count. This is a great opportunity to press on students who seemed to have chosen an arbitrary group size (one pair of students in our class grouped their paper squares by 6s, but because they weren’t comfortable with their multiplication facts for 6, ended up counting by 1s). Other students might need very little press or questioning to realize that they can combine their groups into larger numbers – such as a group of girls who realized they could combine their cups of 5 marbles into cups of 10 marbles, which was more efficient to count by.

Students then record their counts on a recording sheet, which provides more space to show how than to show their answer (for a reason!).  Ultimately, objects get lost or misplaced, so there’s no way of really knowing whether the students were ‘right’ in their counting – this is more about seeing how they’re representing objects and numbers (do they have to draw every object, or can they use numerals as shorthands? Are they adding or multiplying? Can they articulate their thinking in writing yet?).

 

Overall I’m impressed with how the students are doing, and I’m eager to see how they’re able to extend their reasoning from the counting to mental math problems involving multiplication.

Bright Idea: A multiplication 3-act task in a 5th grade classroom

This reflection comes from Connor, who enacted @gfletchy‘s task Array-bow of Colors with 5th graders this past spring.

My instructional goal for this lesson was to have students make the connection between repeated addition and multiplication while solving a problem. Students worked towards this instructional goal in the strategies that they used to solve the problem when working independently and when sharing their answers. I chose the order of responses so that the students would first see how to multiply by breaking the numbers down. Next, they saw how to solve the problem using the traditional algorithm of multiplication. To connect the two multiplication strategies to repeated addition, I had a student discuss how they skip counted to find the answer. The student did not have the opportunity to finish the skip counting, but as a class we discussed how to skip count, which numbers to use, and when to stop.

The Three Act Task started with the students watching the first video. The students noticed many things that I did not notice when I watched the video. For example, one student described that as the skittles were poured into the jar they made a pattern. One other student noticed that the skittles were poured into the jar until it was filled. To extend off of this, and to clarify for the rest of the class, I asked the student where the jar was filled to (to the very top, or to some other point in the jar). I realized after teaching the Three Act Task that I forgot to have students participate in a turn and talk with the person or people sitting next to them. If I taught this lesson again, I would make sure to have students have an opportunity to share their responses with their peers.

After writing down their notices, the students watched the video again and wrote down any wonders that they had. The students participated in a turn and talk with the person or people sitting next to them. The responses that I received were all relevant to the central question. For example, one student asked, “How many wrappers were left over?” Another student asked, “How many bags did he put in the jar?” I was able to make a connection between these two questions, and how they both asked sort of the same thing. The students were able to come up with the central question as one of the wonders. For this three act task, the central question was, “How many skittles were in the jar?”

After writing down the notices and wonders from all the students, I introduced the estimation portion of the lesson. The students were all able to write down a low and high estimate, but some of their estimates could have been better. For example, one student wrote his low estimate as 1. While this is correct, there is a better estimate that he could have written down. When practicing for this lesson, I tried to think of a way to help the students make better estimates. In the video of Graham teaching his Three Act Task, he told the students to, “be brave” when they were making their estimates. If I taught this lesson again, I would try to think of a way to help the students make estimates that were ambitious, but also based on what they already knew.

To move forward from the estimation to solving the problem, I first asked the students how confident they felt about their estimates. Then I asked the students what information they would need to help them make more confident. I phrased the question like this, because even though they are answering the question, how many skittles will it take to fill the jar? The answer is an estimate based on the assumption that there are 14 skittles in each of the bags. The students used the number 14 when solving the problem, but in reality, there were different amounts of skittles in each of the bags. I asked the question to the whole class, but only one or two students raised their hands. To promote more participation, I asked the students to participate in a turn and talk with the person or people sitting next to them. When the class came back together, the students explained that they would need the number of skittles in the bags, and how many bags were used to fill the jar. When giving the students the information, I was careful to state that there were 14 skittles in this bag (the bag that was shown in the picture).

The students also correctly identified that they would need to know how many packages of skittles were used to fill the jar. First I showed the students a picture of a pile of all of the packages and asked them to estimate how many there were. When sharing their responses, the students did not appear to have used a strategy to estimate, and instead just took a guess. To finish this portion of the lesson, I showed the students how many packages were actually used (58). The students began to work on answering the question.

When I circulated around to observe what strategies the students were using, I noticed that there were three main ones.

The first, and most common strategy that students used was to set up a vertical multiplication problem with one number on top of the other. While many students were able to set up the problem correctly, not many were able to get the correct answer. After teaching my lesson, I found out that the students have not learned how to do double digit multiplication using the traditional algorithm. In their work, the students would multiply one digit by the other two (for example in 58 x 14 the students would multiply the 4 by the 8 and 5), but would not finish the problem by multiplying the other digits together. In addition, one of the other challenges that students had with using the traditional algorithm was that they had trouble lining up the digits to get a correct answer. Even if the students multiplied the digits correctly, when figuring out their answer, the students would not line up the numbers correctly, and as a result would not get the right answer. To help students understand how to use the traditional algorithm correctly, when sharing answers, I made sure to talk about the place value of each of the digits in the number. I also walked the students through the multiplication process and how the algorithm was used in this problem. My teacher told me that the students will be learning how to use the traditional algorithm soon, because it is on the state test in the beginning of May.

Another common strategy that students used to help them solve the problem was to break one of the numbers up and then to multiply it by the other number. For example, when implementing this strategy, one student broke 58 into 50 and 8. Then he divided each number by 14 and added the products. The student got the correct answer using this strategy.

One last strategy that some students used was skip counting. The students used this strategy most often to add 14 together 58 times. When sharing this strategy with the students, one identified that while this strategy works, it takes a long time, and can be hard to add together. Based on this, I asked the students if skip counting and repeated addition would only work with 14. The students replied that they could use the same strategy for 58, but also explained to me that it is harder for them to add 58 together 14 times. I tried to connect the repeated addition strategy that was used to the two multiplication strategies by reviewing one of the claims that was made in the mental math. In the mental math, one student explained that repeated addition was a longer way of doing the multiplication. To review that in my lesson, I asked the students what numbers they used in the addition sentence, and how this connected to the multiplication that was done earlier. The students were able to identify the connection that they discovered in the mental math.

At the end of the lesson, I revealed the answer to the students. They were confused as to why the answer that Graham Fletchy got was different from their answer. To help them understand why, I offered up a situation where two of the students have the same brand, size and type of chips. I asked the students if each of the bags would have the same number of chips. Some students still appeared confused by this situation, but others began to understand what I was saying. One student explained that if they counted to make sure that every bag of chips had the same number of chips in it, the factories would not make that many bags each day. Transitioning back to the lesson, I asked the students how they could connect the chip scenario to the skittles. One student raised her hand and said that just like the bags of chips, each package of skittles would not have the same amount of skittles in it. Going off of this, I explained that we only knew how many skittles were in the first package, and not how many were in each of the other bags.

To finish my lesson, I gave the students an exit ticket, asking them to determine how many skittles were in a case of skittles that was pictured on their exit ticket. The students were given the number of skittles in one package, and how many packages were included in the case. From this, the students solved the problem again. One of the changes that I saw between the work they did in the lesson and the work they did on the exit ticket, is that more students used the second strategy on the exit ticket. Many of the students broke up the number 36 into 30 and 6, then tried to do the multiplication. However, some students still seemed stuck when they went to multiply 56 x 30.

From this lesson, I learned that my students can apply previous strategies that they have learned to new situations. In this lesson, I was not teaching the students any new strategies, or ways to solve a problem. Rather, I was seeing how well they can apply strategies and techniques that they have learned already. The students proved they were able to do this by using the multiplication strategy that my host teacher taught them earlier in the year, and by relying on their knowledge of skip counting.

I also learned from this lesson that my students need some strategies to help them make more educated estimates. In the lesson, the students first made estimates about how many skittles they thought would fill up the jar. The students’ estimates were not always realistic, and many of the students put estimates that were safe. For example, when asked to write a low estimate of how many skittles would fill up the jar, many students wrote down 1. While this is correct, there were other, higher numbers that could have been used that were more ambitious. The students next used estimation when trying to figure out how many packages of skittles were used to fill up the jar. The students guessed estimates that again did not seem realistic. When asked how they came up with their estimates, none of the students had a strategy that they used. Instead, it became clear to me that the students were just guessing how many packages were used.

If I were to teach this lesson again, I would change the way that I wrote down the notices and wonders. In my lesson, I set up two pieces of paper in the back of the room where I wrote down the notices and wonders. However, because of the placement of the papers that I was writing on, the students had to turn around in their seats to look at me. This led to many students not looking at me when I was teaching, and students having to turn around every time that I wanted to talk to them. One other thing that I would change about the notices and wonders section, is that I would write them neater, and also larger. I noticed after writing down the notices is that they were very small. I tried to write larger when writing down the wonders, but they could have been neater. One of the problems that I ran into, was that I did not want to turn my back on the students for too long.

If I were to teach this lesson again, I would also try to ask more questions about the strategies that students used. While I asked questions about the strategy that was used, looking back, I should have started with more basic questions like, “How did you know to multiply 58 and 14 together?” This would have allowed every student to understand the strategy before moving on to more complicated questions that would establish connections between the strategies.

If I were to teach this lesson again, I would also ask the students to draw a picture of the problem. This was not a central focus of my lesson, so I did not emphasize it as much as I should have. Creating a visual representation of a problem is important because it helps students make sense of the problem. I decided not to push the students to draw a picture of the problem because it was not a strategy that I saw the students using. I did not know how to introduce this strategy, or if it was something that I should introduce. Instead, I decided to focus more on the strategies that I saw students using.

Based on this lesson, the next choral count, mental math, or Three Act Task that I taught would be focused on connecting a picture of a problem to repeated addition and multiplication. After the sequence of lessons that I taught, I am confident that students understand the connection between repeated addition and multiplication. In my next lesson, I would try to extend that connection to creating a visual representation of the picture. This would help students make sense of the problem that they were trying to solve, as well as seeing how repeated addition and multiplication are used, and where each of the numbers in the number sentences comes from.

 

The Final Lap: Comparing and ordering decimals in a 5th grade classroom

 

Amanda is teaching 5th grade this semester at a local elementary school and recently got to enact the Final Lap task (created by Graham Fletcher) with her students.  Note that Amanda changed the finishing times of the NASCAR cars to minutes, and limited the times to numbers in the hundredth place.

The instructional goal for this lesson was for students to compare decimals to hundredths by reasoning about their size and to recognize that comparisons are valid only when the decimals refer to the same whole. In lessons prior to this, students were introduced to decimals to tenths and hundredths and changing fractions into decimals/decimals into fractions. This lesson introduced students to comparing decimals. Another goal of mine was for students to understand how and why decimals are used. Some students were having difficulty understanding when we use decimals and the importance of them. Showing students a NASCAR race where the times of each car are given as decimals proves that decimals are used in everyday life, for various reasons, and assist us with tasks that must be completed. Therefore the instructional goals of this lesson were met because students compared real life race times (which helped them understand the usage of decimals) and ordered them from smallest to largest/first place to last place.

In the beginning of the lesson, the class created a notice and wonder chart about the NASCAR 3-Act Task video.

I anticipated that students would notice the numbers on the cars, which was good because that’s how we spoke about each of the cars (which got tricky when we added in the decimals we were working with. It was a lot of numbers to write and speak about). Also, I anticipated that a student would wonder, “why are we watching this video” and “who won the race”. This question – who won? – was the first one students asked, and the most to get the “me too!” symbol (sign language we use in class), which made it easy to come back to and highlight as our main question.  During the creation of our chart I did not anticipate a notice about the decimals in the right-hand corner of the screen. Hearing this I was surprised because to be honest I did not catch this the first few times I watching the video by myself. When a student mentioned this as his notice I told him, “Speaking about decimals, I want everyone to keep everything they know about decimals in the front of their brain because it will come in handy.” I did not want to give away anything but I wanted the other students to start thinking about decimals and recalling prior knowledge/lessons.

Once we created a class notice and wonder chart, I asked the students what information/tools do we need to solve this problem. I anticipated the responses would be the lineup of cars and the amount of time each car finished the race. Instead, the only two responses I got were “more of the video” and “a picture of the finish line”.

 

 

This probed me to say, “Let’s say technology was not working and the announcers had to take notes of the race. What would we want to see and in their notes?”. I still got answers such as, “the car that won” and “description of which car won and how” but I also got the following response, “which cars finished the race” which lead to “how fast each car finished the race”. Although these weren’t the exact responses, they aligned with the information they needed to solve the problem and what I had to share with them.

When I shared the information with the students I planned that some of them would know the answer right away. Predicting this, I told the students that if they knew the answer please be respectful and keep it in their minds, but if they wanted to share then they would have to use their whisper phones to let it out. During the enactment of the lesson there were students who were so excited they knew who won that they had to let it out so they used their whisper phones. This allowed students to not spoil the answer or persuade any of their peers’ thinking. Having students know the answer right away also led me to stating clear directions of, “proving your answer with work and using the decimals to do so” and extension questions that were as followed, “put the cars in order from 1st to 7th place”, “how many seconds did 1st place win by”, and “how many seconds did the 1st place car beat the 7th place car”.

Starting with the Notice and Wonder chart, I learned that it is a great activity for every single one of my students. Since this activity is “low floor, high ceiling,” students of all skill level can participate. For example, my student that rarely speaks in class due to language disconnect shared a notice about the color of the cars. Also, a student that is usually disengaged during the math block was the student that shared our wonder question, “Who won the race?”. I learned that if you give students the chance to show their knowledge from the very beginning of the lesson they will be more inclined to participate throughout the whole lesson/unit.

Also, I learned that my students are taught to think of math as a question and answer process. From the time that I stated the main question, most of the students were obsessed with getting the right answer. They asked, “what does this video have to do with the math were doing today?” and “Am I right?”. Even during independent work time, multiple students raised their hands just to ask, “Did I get the right answer?”. When I wouldn’t tell them or show them the final answer right away they got frustrated and questioned their work even though it was right. These reactions show me that my students are not regularly learning to value the process and instead focus on the correct answer or algorithm that will get them the “A” or “100 %”.

 

While sharing strategies, I learned that the students are most comfortable with thinking about whole numbers. Almost all of the students used strategies that sorted the times according to whole number then made a data table from smallest to largest or data table with the smallest whole numbers on top then the largest on the bottom and then wrote 1st, 2nd, 3rd,… next to the times. Also, while sharing their strategies, they called numbers to the left of the decimal whole numbers but they didn’t seem to have a name for the numbers for tenths and hundredths. Some students used these terms without probing, but most students caught on to tenths and hundredths after I went over the terms by showing them the following layout, “whole numbers. tenths hundredths”.

If I were to teach this lesson again, I would do a mini lesson prior to the 3 Act Task. This mini lesson would be on place values including decimals. I would have the students write any decimal they like (keeping it to no more than 3 numbers), write that decimal exactly how they would say it aloud, and then turn and share their number with a partner. This activity would allow for the students to have a productive struggle of what to call each place value. After a class discussion, I would show the students the actual decimal place value system. This would look like “whole numbers . tenths hundredths” or “hundreds tens ones . tenths hundredths”. Students could refer to this place value chart during the 3 Act Task and future decimal lessons. I would include this mini lesson prior to the 3 Act Task because when speaking about the times of each car students would say “26 point 23” or “the first/second number after the decimal”. It wasn’t only until I stopped the lesson to draw and explain the decimal place value system that they started using the language “tenths” and “hundredths”. Some students still fell back to the “26 point 23” or “first/second number after the decimal” but this tells me that they don’t fully understand what the tenths and hundredths represent. Therefore, with these specific students I would have to go deeper into exploring the decimal place value system. If I would have done the mini lesson I think students would understand tenths and hundredths which would have made the task easier to understand, contextualize, and more fluid.

Another change I would make is how I asked the students to show their work. I wish I would have asked the students at first to order them from 1st to 7th place instead of making that an extension problem. I would do this because it would force students to interact with the decimals from the beginning and not just use mental math to figure out who won. Also it would give me more time to focus on strategies because I wouldn’t have to go up to each student who finished and ask them the first extension question.

Based on how the lesson what I would conduct a number talk and have students compare 25.3 and 25.29. This question was my exit ticket, but I ran out of time to hand it out. I would choose this specific problem because I want to see which students understand the place values of tenths and hundredths, and whether they can compare the number of digits with the value of each digit. Also, it would encourage them to recall the names of the place values and use them to describe their thinking.

 

 

The Apple Task: Enactment artifacts from a 5th grade classroom

On 3/3/17, I was able to work with an outstanding group of 5th graders at a local elementary school on one of my favorite 3-act tasks by Graham Fletcher – The Apple.

The Apple gets students thinking about division as measurement, and if left to solve the problem in a way that makes sense to them, they tend to generate a range of strategies that can be really useful stuff for making connections in a pre-reveal discussion about their strategies. In particular, this task is useful for making connections between:

  • repeated addition (adding one block at a time until we ‘arrive’ at the apple’s weight)
  • repeated subtraction (taking off a block’s-worth of weight from the apple until we ‘arrive’ at zero)
  • multiplication (often in the form of guess and check after students grow weary of repeated addition), and
  • fraction division using the common denominator method (get a common denominator and divide the numerators).

We started by playing the video for students and asking them what they noticed and wondered. As they shared, we recorded their noticings and wonderings on chart paper:

As a class, we decided on the starred question as the one to solve for the day. Once we’d come to consensus (using words and gestures) for what it would mean to balance the scale,  we asked students to estimate the number of blocks it would take. We recorded their estimates.

 

We then asked students what information they would need to solve this problem – and why they would need it. Most students suggested fairly quickly that we would need to know the weight of the blocks and the weight of the apple – but I asked several students to argue for why we needed both and not just one. This took some time, but by the end it seemed most students understood why both weights were important, and what significance they had mathematically and contextually.

Then, we gave them the information. (I wrote the info down in the wrong ‘spots’ on the “what do we need to know” chart at first, so I had to rewrite.)

Once we gave them this information, we gave students about 2-3 minutes to begin a strategy on their own piece of paper – enough time to make a plan, but not enough time to follow it all the way through.

After a few minutes passed, we asked them to talk to the other students at their tables and discuss their strategies, and come to a decision about how they would use one or more of the strategies at their tables to solve the problem. They were also tasked with representing one strategy on a group white board. Here’s what those white boards looked like by the end:

 

 

 

 

 

Multiplication strategy: what number multiplied by 3/8 gets us 5 and 2/8?

 

These students started by repeatedly adding 3/8 until they grew weary of it, and decided to start multiplying. They tried 1, 2, 3, 5, 10, 13, and then finally did 13 blocks plus 1 more block.

 

Repeated addition of 4 blocks at a time.

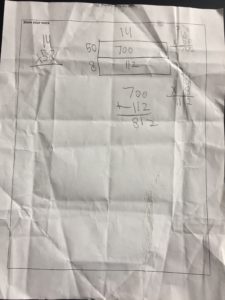
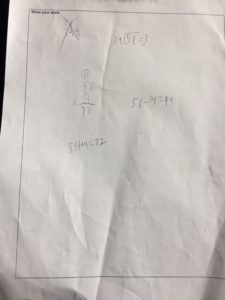
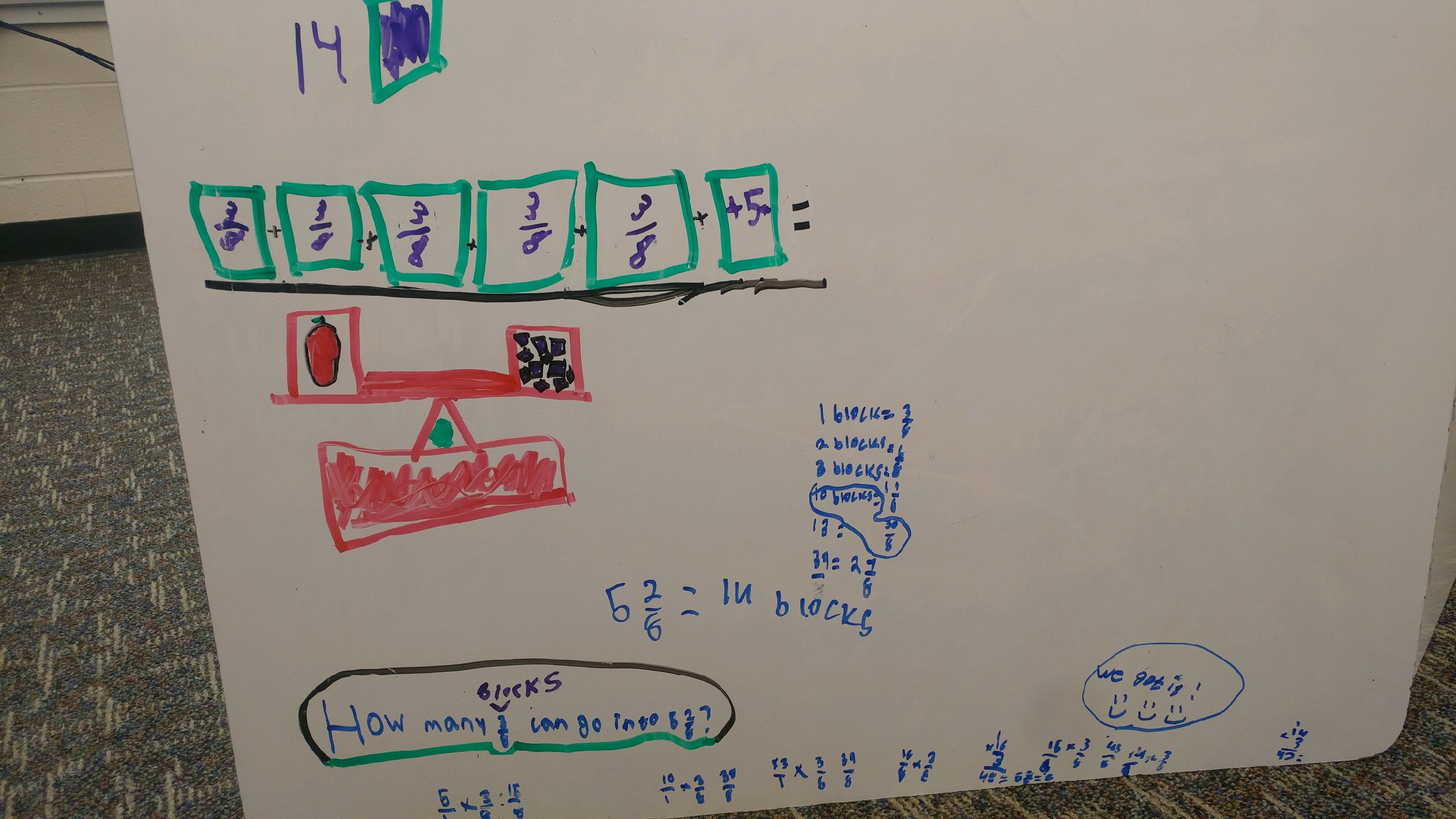
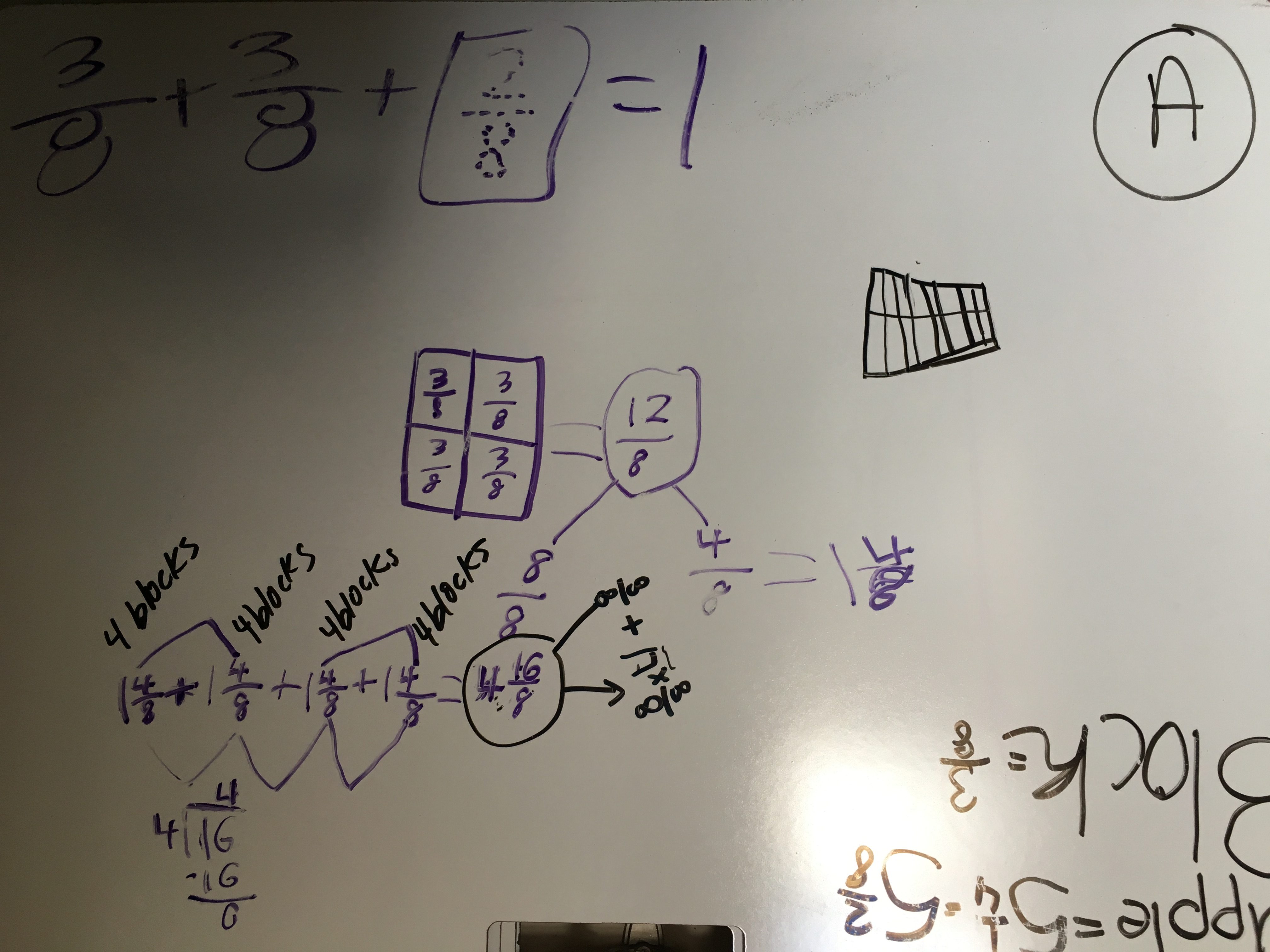I LOVED this strategy. This group was led by two students in particular whose really wanted to find a combination of blocks that would add up to an easy ‘split.’ So they settled on 4 blocks, since 4 groups of 3/8 makes 12/8, which would only need 1/2 an ounce to get to the next whole. They knew, then, that two groups of 4 blocks would ‘make up’ the next whole.

Once they started down this path, however, they found themselves in improper fraction land quite quickly, which it turned out was not a land they had adventured in many times before. Out of the 4 students in the group, 3 of them were quite insistent that 4 and 16/8 oz (which they arrived at by repeatedly adding 4 blocks 4 times – so, 16 blocks) was not yet enough weight to equal the apple. They had some difficulty moving past this moment, and ran out of time to come to consensus as a group about what should happen next – though they agreed that it would likely entail adding single blocks to finally get to 5 1/4 oz, since most of them were sure that 4 more would be too many.

 

Repeated addition, using a choral count representation

This was a strategy we were really hoping would turn up, since the students had just done a choral count by 1/8 in the moments preceding the 3-act task. Interestingly, this strategy did not represent the first strategy all of the students in the group had used; several had used a division strategy, but because they could not figure out how to represent or explain how that strategy worked (which was what we insisted they be able to do with any strategy they put on their board), they resorted to using a repeated addition strategy. The challenging thing in this group’s case was figuring out in all of this representation where the answer was.

In addition to these three group boards, there was one last group who had worked hard to find solution strategies independently, but who had run out of time to get much onto their board before we discussed strategies:

The students had about 20 minutes in their groups to produce the representations above, and then we took about 10 minutes to look across the first three boards above, first looking at the choral count strategy, then the repeated addition of 4 blocks, then finally the multiplication strategy. The questions I asked of each group were –

  • where is the apple represented in this group’s strategy?
  • How did they know where to stop?
  • What were they looking to have happen by [adding 1/8 at a time…adding 4 blocks at a time…multiplying numbers by 3/8]
  • How did they know they had done enough?
  • Based on all of this work, what is the group’s answer to the question?

Though I’m not confident that all of the students came to consensus about whether or why multiplication was more efficient than repeated addition, they all agreed that in this case, anyway, it produced the same result. The group who was adding ‘batches’ of 4 blocks at a time seemed to understand by the end that their method was functioning pretty well, but that it might require more adjustment because of undershooting or overshooting the perfect amount – a problem the choral count group didn’t have, but that the multiplication group did (they found that 13 was close, so they adjusted from there).

Afterward, we gave them exit tickets to see how they would solve a related problem – and to see how they were making sense of the fraction 3/8 as it relates to 1. Here are a few examples of student work :

 

All in all, this task was a great way to feel out students’ thinking about the relationships between addition, subtraction, multiplication, and division, and whether those relationships behave predictably with fractions. It was also a great way to peek into how students are marshaling procedures like finding a common denominator as steps to solving a problem, rather than as a procedure for it’s own sake. It’s clear that we have more work to do to build common understanding about some of these ideas, but I loved the opportunity we got to ask students to completely fly blind into material they’ve never ventured into before, and see what sense they made of it.